Mathematics
The following figure shows a solid of uniform cross-section. Find the volume of the solid. All measurements are in centimetres. Assume that all angles in the figure are right angles.
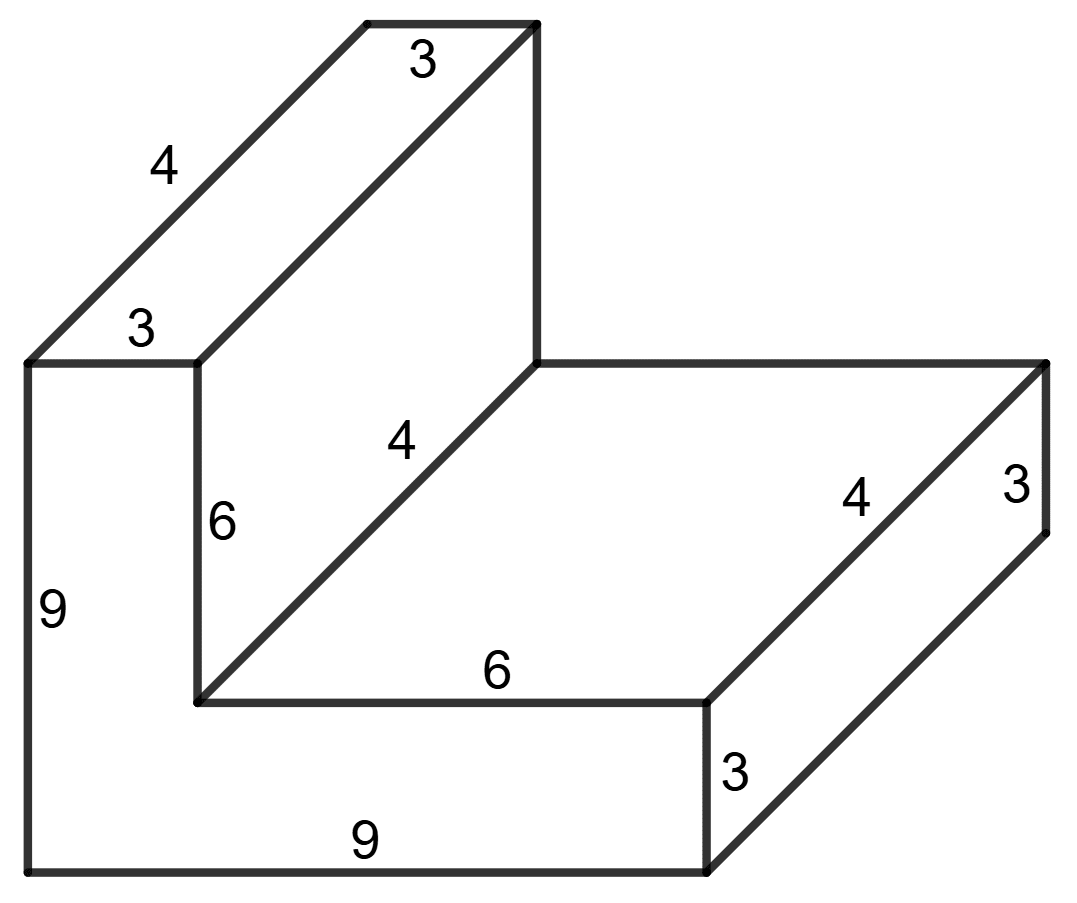
Mensuration
28 Likes
Answer
The solid can be divided into two cuboids.
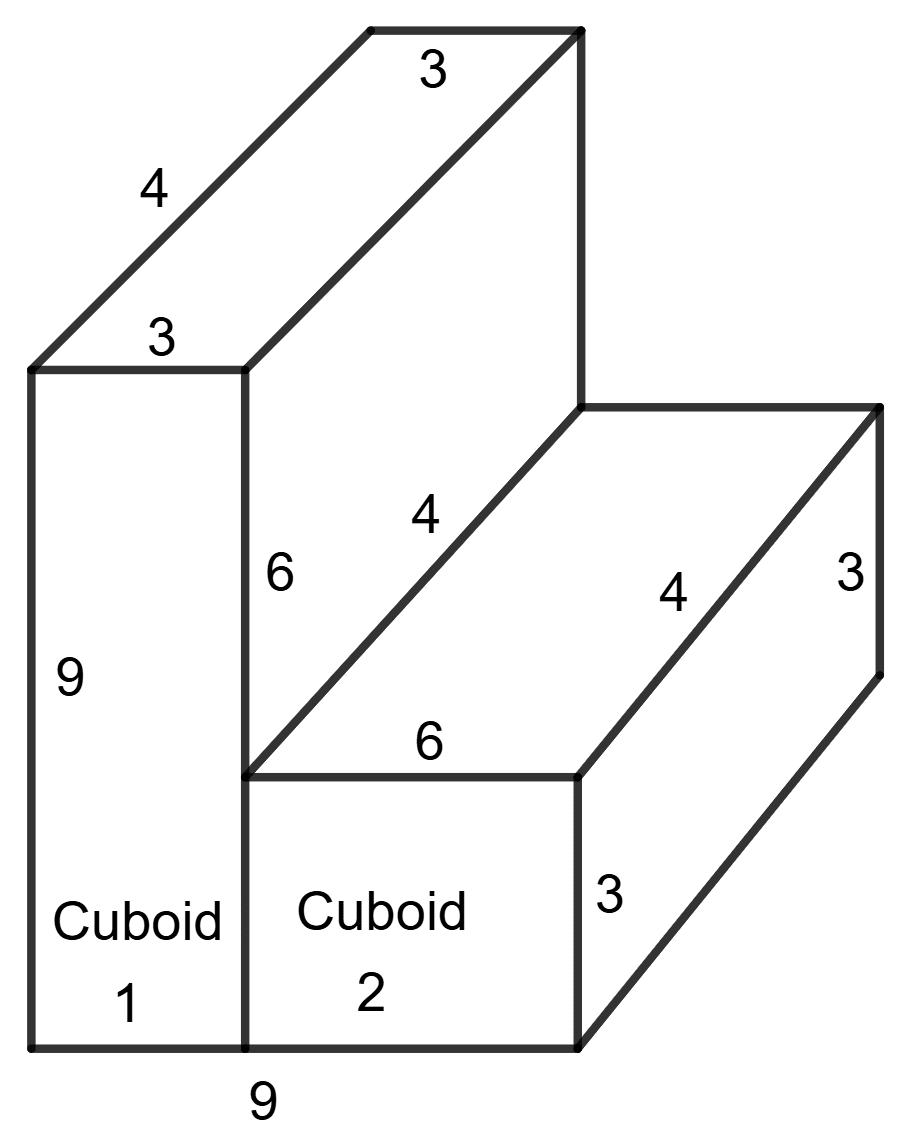
Dimensions of cuboid 1:
Length(l1) = 9 cm Breadth(b1) = 4 cm Height(h1) = 3 cm
Dimension of cuboid 2:
Length(l2) = 6 cm Breadth(b2) = 4 cm Height(h2) = 3 cm
Volume of solid = V1 + V2
= l1b1h1 + l2b2h2
= 9 x 4 x 3 + 6 x 4 x 3 cm3
= 108 + 72 cm3
= 180 cm3
Hence, the volume of the solid is 180 cm3.
Answered By
21 Likes
Related Questions
A closed rectangular box is made of wood of 1.5 cm thickness. The exterior length and breadth are respectively 78 cm and 19 cm, and the capacity of the box is 15 cubic decimetres. Calculate the exterior height of the box.
The square on the diagonal of a cube has an area of 1875 sq. cm. Calculate :
(i) the side of the cube.
(ii) the total surface area of the cube.
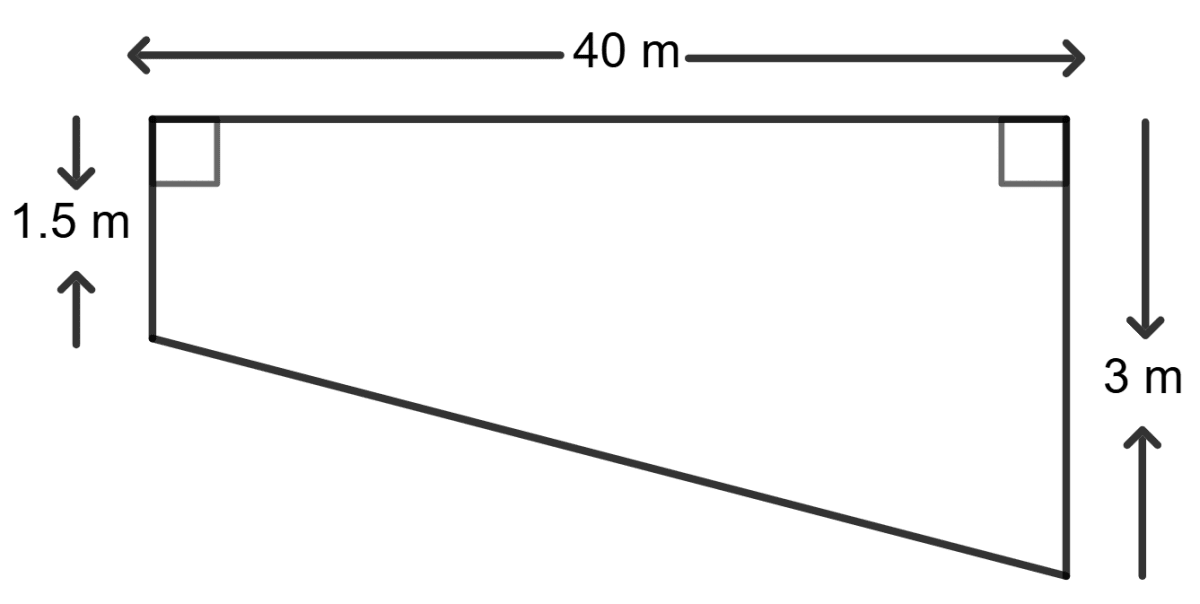
A swimming pool is 40 m long and 15 m wide. Its shallow and deep ends are 1.5 m and 3 m deep respectively. If the bottom of the pool slopes uniformly, find the amount of water in litres required to fill the pool.
The cross-section of a tunnel perpendicular to its length is a trapezium ABCD as shown in the following figure; also given that : AM = BN; AB = 7 m; CD = 5 m. The height of the tunnel is 2.4 m. The tunnel is 40 m long. Calculate :
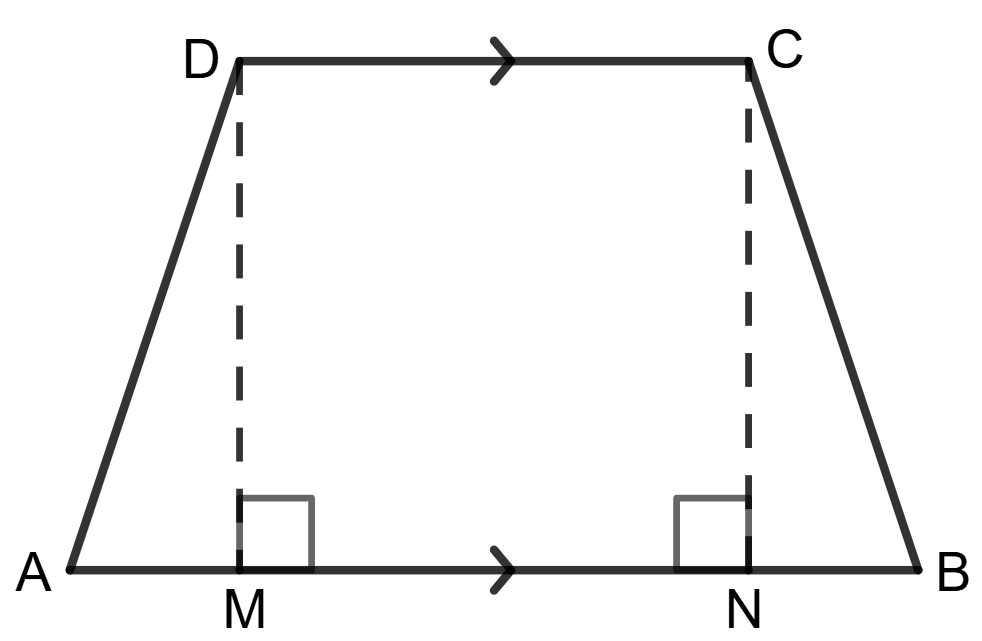
(i) the cost of painting the internal surface of the tunnel (excluding the floor) at the rate of ₹ 5 per m2 (sq. metre).
(ii) the cost of paving the floor at the rate of ₹ 18 per m2.