Mathematics
Draw an ogive for the following distribution :
| Income in ₹ | No. of employees |
|---|---|
| 120 - 140 | 30 |
| 140 - 160 | 72 |
| 160 - 180 | 90 |
| 180 - 200 | 80 |
| 200 - 220 | 70 |
| 220 - 240 | 28 |
Use the ogive drawn to determine :
(i) the median income,
(ii) the number of employees whose income exceeds ₹ 190.
Statistics
24 Likes
Answer
Cumulative frequency distribution table :
| Income in ₹ | No. of employees | Cumulative frequency |
|---|---|---|
| 120 - 140 | 30 | 30 |
| 140 - 160 | 72 | 102 (30 + 72) |
| 160 - 180 | 90 | 192 (102 + 90) |
| 180 - 200 | 80 | 272 (192 + 80) |
| 200 - 220 | 70 | 342 (272 + 70) |
| 220 - 240 | 28 | 370 (342 + 28) |
(i) Here, n = 370, which is even,
Median = = 185.
Steps of construction :
Take 2 cm = ₹ 20 on x-axis.
Take 1 cm = 50 employees on y-axis.
A kink is shown near x-axis as it starts from 120. Plot the point (120, 0) as ogive starts on x-axis representing lower limit of first class.
Plot the points (140, 30), (160, 102), (180, 192), (200, 272), (220, 342) and (240, 370).
Join the points by a free-hand curve.
Draw a line parallel to x-axis from point H (no. of employees) = 185, touching the graph at point I. From point I draw a line parallel to y-axis touching x-axis at point J.
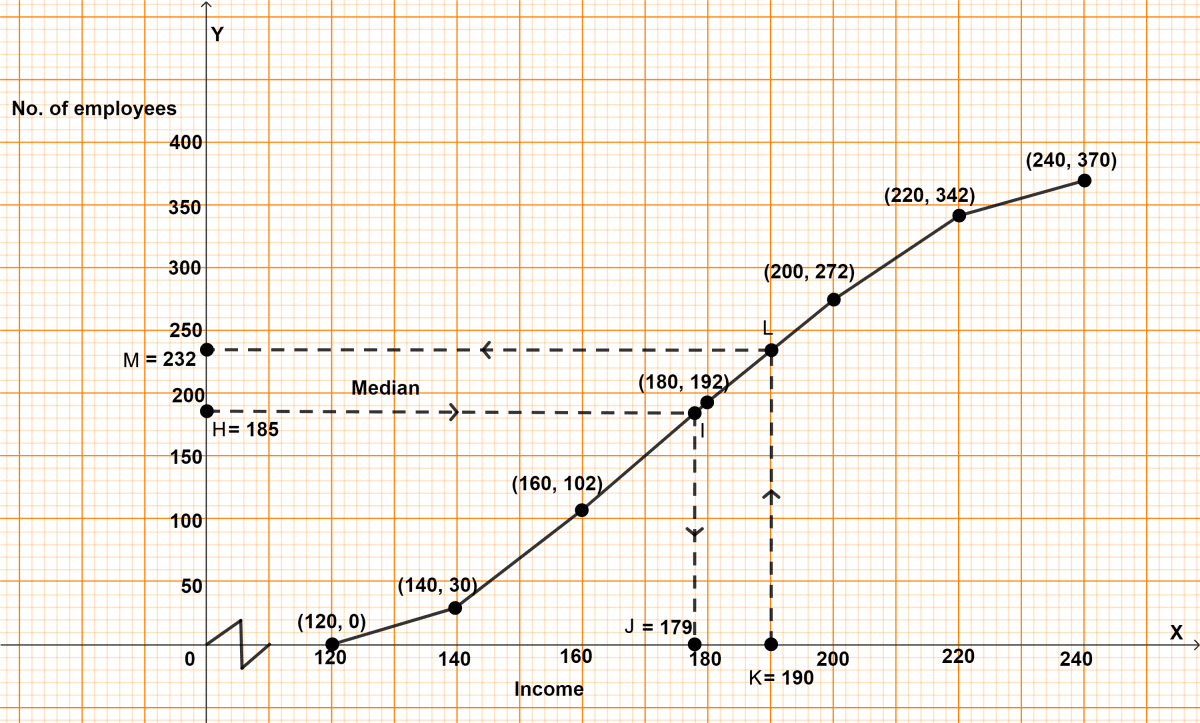
From graph, J = 179
Hence, median wage = ₹ 179.
(ii) Steps :
- Draw a line parallel to y-axis from point K (income) = ₹ 190, touching the graph at point L. From point L draw a line parallel to x-axis touching y-axis at point M.
From graph, M = 232
It means that,
232 employees have income less than or equal to ₹ 190.
∴ No. of employees having income more than ₹ 190 = 370 - 232 = 138.
Hence, no. of employees having income more than ₹ 190 = 138.
Answered By
9 Likes
Related Questions
Draw an ogive for the data given below and from the graph determine :
(i) the median marks,
(ii) the number of students who obtained more than 75% marks ?
Marks No. of students 10 - 19 14 20 - 29 16 30 - 39 22 40 - 49 26 50 - 59 18 60 - 69 11 70 - 79 6 80 - 89 4 90 - 99 3 The incomes of the parents of 100 students in a class in a certain university are tabulated below.
Income (in thousand ₹) No. of students 0 - 8 8 8 - 16 35 16 - 24 35 24 - 32 14 32 - 40 8 (i) Draw a cumulative frequency curve to estimate the median income.
(ii) If 15% of the students are given freeships on the basis of the income of their parents, find the annual income of parents, below which the freeships will be awarded.
(iii) Calculate the Arithmetic mean.
The result of a examination is tabulated below :
Marks (less than) No. of candidates 10 0 20 25 30 42 40 65 50 95 60 120 70 128 80 135 90 148 100 150 Draw the ogive for the above data and from it determine :
(i) the number of candidates who got marks less than 45.
(ii) the number of candidates who got marks more than 75.
Marks obtained by 200 students in an examination are given below :
Marks No. of students 0 - 10 5 10 - 20 11 20 - 30 10 30 - 40 20 40 - 50 28 50 - 60 37 60 - 70 40 70 - 80 29 80 - 90 14 90 - 100 6 Draw an ogive for the given distribution taking 2 cm = 10 marks on one axis and 2 cm = 20 students on the other axis. Using the graph, determine :
(i) The median marks
(ii) The number of students who failed if minimum marks required to pass is 40 ?
(iii) If scoring 85 and more marks is considered as grade one, find the number of students who secured grade one in the examination ?