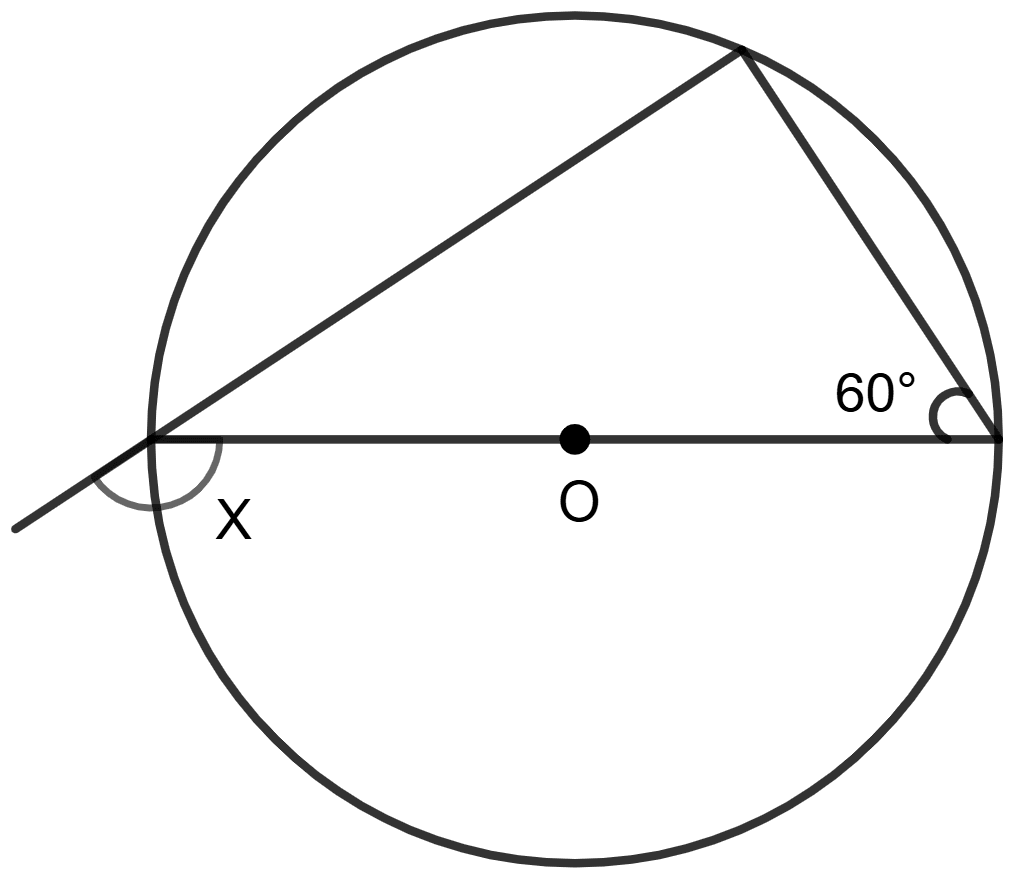Mathematics
From an external point P, the tangent PA is drawn to the circle with centre O.
(i) If OP = 20 cm and tangent PA = 16 cm find the diameter of the circle.
(ii) If diameter of the circle is 20 cm and tangent PA = 24 cm, find the length of OP.
Circles
7 Likes
Answer
O is center of the circle. PA is the tangent of the circle.
We know that,
Tangent and radius through the center at point of contact are perpendicular to each other.
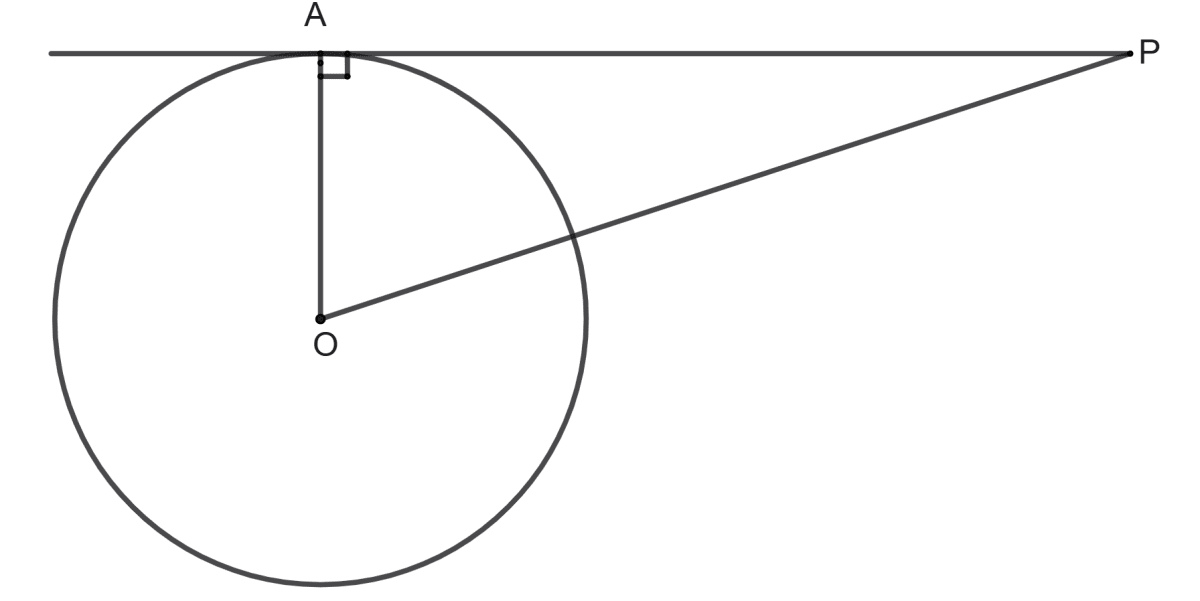
(i) Given, OP = 20 cm and PA = 16 cm
In the ∆OPA as we know that ∠OAP = 90°.
As we know Pythagoras theorem can be used in a right angled triangle,
⇒ OA2 + PA2 = OP2
⇒ OA2 + 162 = 202
⇒ OA2 + 256 = 400
⇒ OA2 = 400 - 256
⇒ OA2 = 144
⇒ OA =
⇒ OA = 12 cm
By formula,
Diameter = 2 x radius = 2 x 12 = 24 cm.
Hence, the diameter of the circle = 24 cm.
(ii) Given, diameter = 20 cm and PA = 24 cm
Radius (OA) = = 10 cm
In the ∆ OPA as we know that ∠OAP = 90°.
As we know Pythagoras theorem can be used in a right angled triangle,
⇒ OA2 + PA2 = OP2
⇒ 102 + 242 = OP2
⇒ 100 + 576 = OP2
⇒ OP2 = 676
⇒ OP =
⇒ OP = 26 cm.
Hence, the length of OP = 26 cm.
Answered By
3 Likes
Related Questions
The following figure shows a circle with centre O and diameter PQ. Point R lies on the circumference of the circle such that PR = QR and PR = 4 cm.
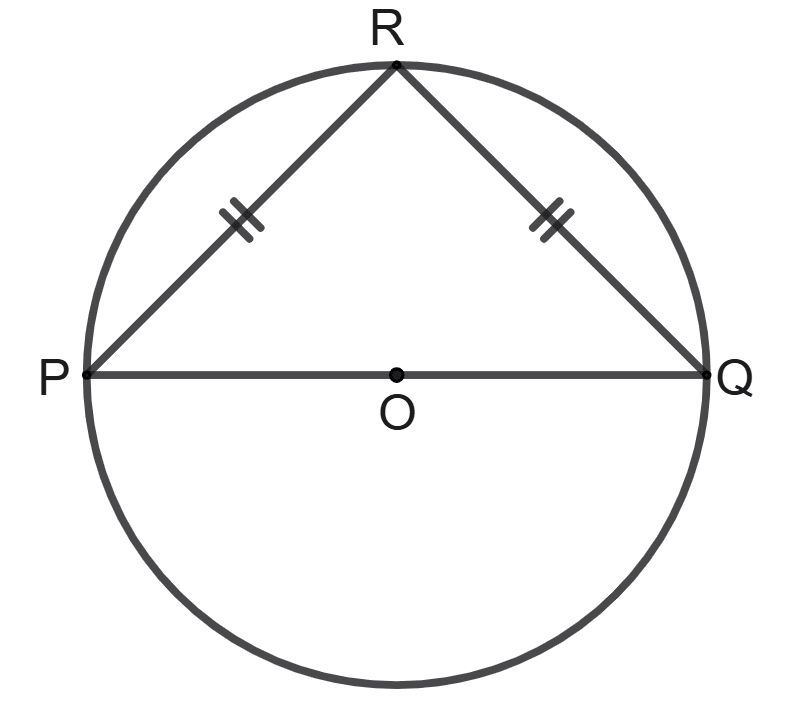
Calculate the radius of the given circle and state its value correct to two decimal places.
In the following figure, PQ and PR are the tangent to the circle with centre O. Line segment AC touch the circle at point B.
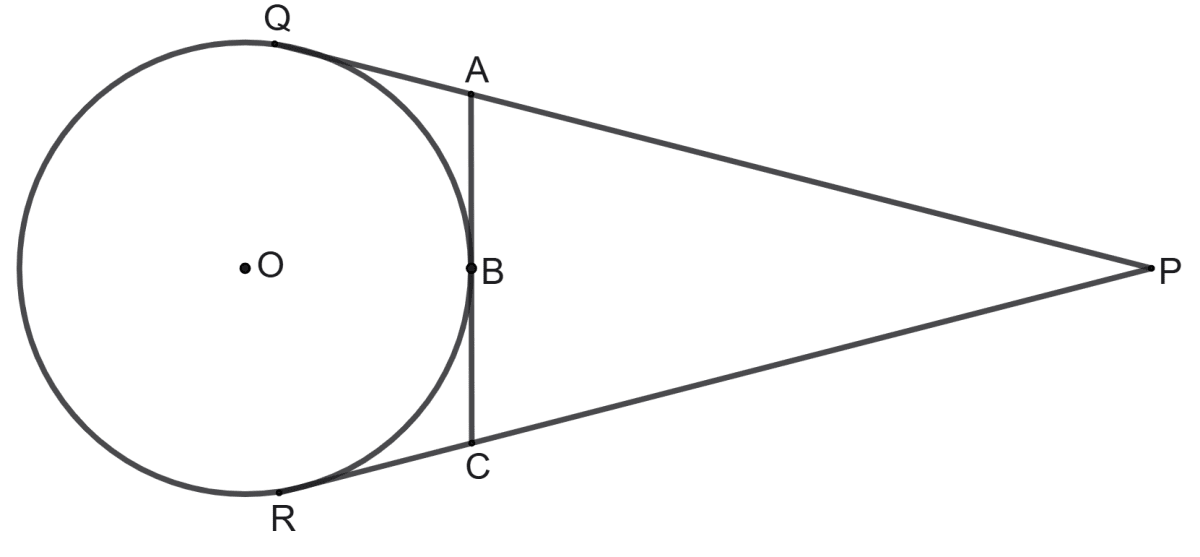
(i) State the relation between tangent PQ and PR.
Also show that:
(ii) PQ = PA + AB
(iii) PR = PC + CB
(iv) PQ + PR = Perimeter of ΔPAC.
In figure given below, O is the centre of the circle, use the given information to find the value of x:
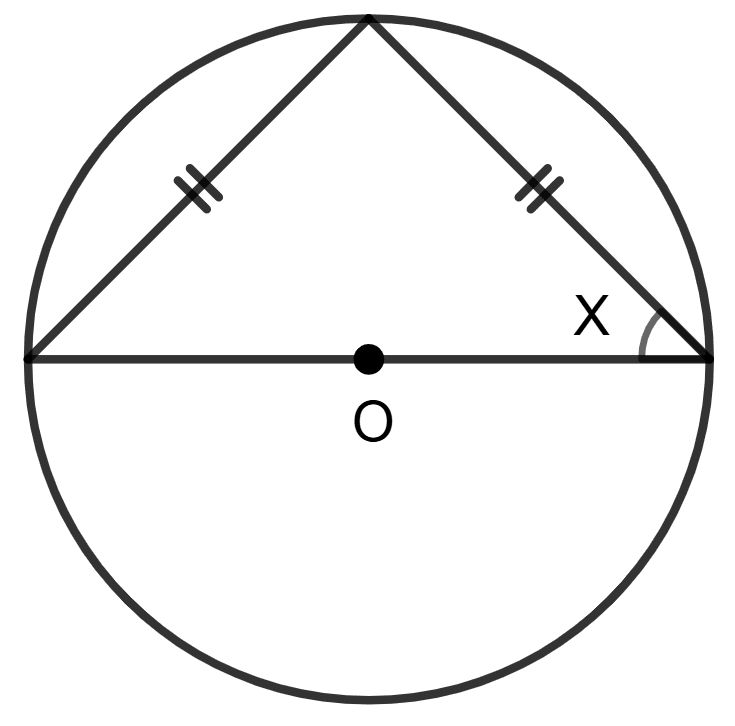
In figure given below, O is the centre of the circle, use the given information to find the value of x: