Find the area and the perimeter of the following figure.

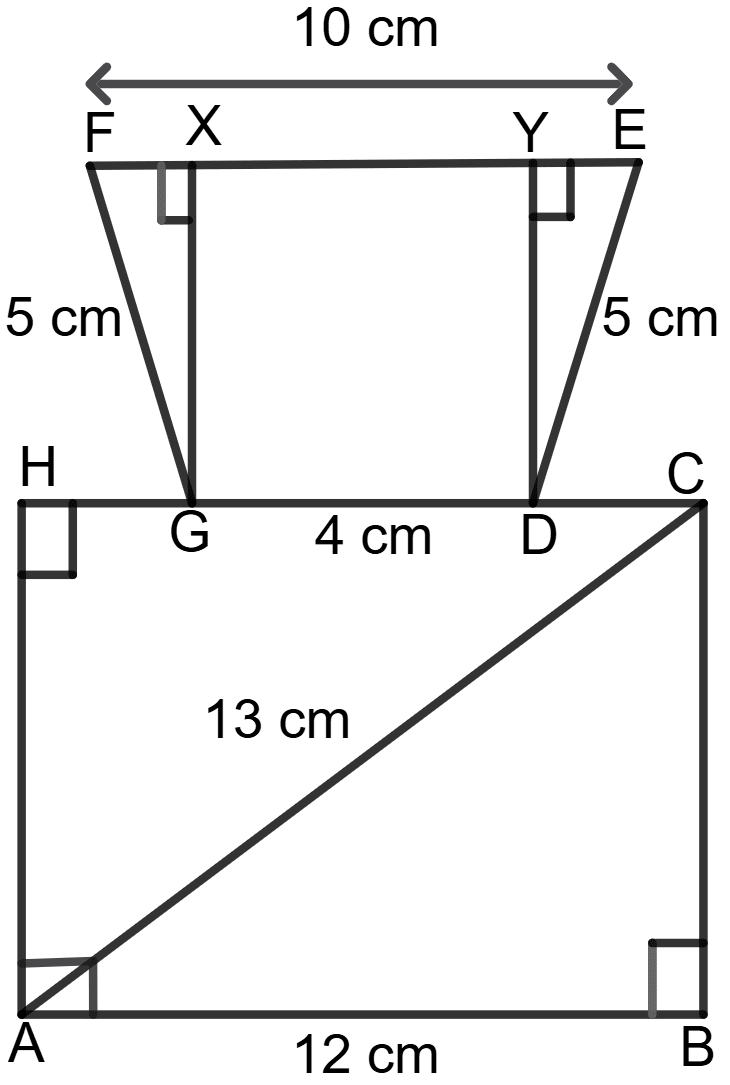
Given : AB = 12 cm, AC = 13 cm, DE = FG = 5 cm, EF = 10 cm and GD = 4 cm.

As △ABC is a right angled triangle, using pythagoras theorem:

⇒ AC² = AB² + BC²

⇒ 13² = 12² + BC²

⇒ 169 = 144 + BC²

⇒ BC² = 169 - 144

⇒ BC² = 25

⇒ BC = $\sqrt{25}$

⇒ BC = $\pm$ 5

(Since length cannot be negative, we take the positive value.)

BC = 5 cm

Perimeter of the figure = AB + BC + CH + DE + EF + FG + HA - GD

= 12 + 5 + 12 + 5 + 10 + 5 + 5 - 4

= 50 cm

Area of figure = Area of rectangle ABCH + Area of quadrilateral DEFG

Area of rectangle ABCH = length x breadth

= AB x BC

= 12 x 5 = 60 cm²

Consider GDEF as a trapezium with EF ∥ GD. Draw GX ⊥ EF and DY ⊥ EF.

In ΔFXG and ΔEYD,

FG = ED (Given)

∠FXG = ∠EYD = 90°

GX = DY (Perpendiculars between two parallel lines are equal in length)

By SAS congruence criterion,

ΔFXG ≅ ΔEYD

FX = EY (By CPCT)

XY = GD = 4 cm.

EF = XY + FX + YE

10 = 4 + FX + YE

FX + YE = 6 cm

FX = YE = $\dfrac{6}{2}$ = 3 cm

In ΔFXG, using pythagoras theorem,

FG² = FX² + GX²

⇒ 5² = 3² + GX²

⇒ 25 = 9 + GX²

⇒ GX² = 25 - 9

⇒ GX² = 16

⇒ GX = $\sqrt{16}$ = 4 cm

Area of trapezium GDEF = $\dfrac{1}{2}$ x (Sum of parallel sides) x height

= $\dfrac{1}{2}$ x (GD + EF) x GX

= $\dfrac{1}{2}$ x (10 + 4) x 4

= $\dfrac{1}{2}$ x 14 x 4

= 7 x 4 = 28 cm²

Area of figure = Area of rectangle ABCH + Area of trapezium GDEF = 60 + 28 = 88 cm²

Hence, perimeter of the figure = 50 cm and area of the figure = 88 cm².