Mathematics
The first term of an Arithmetic Progression (A.P.) is 5, the last term is 50 and their sum is 440. Find:
(a) the number of terms
(b) common difference
AP
18 Likes
Answer
Given,
First term a = 5, last term l = 50, and sum of terms Sn = 440
(a) Let the Number of terms be (n),
Formula for sum of an A.P.:
Hence, the number of terms is 16.
(b) Let the Common difference be (d),
Formula for nth term:
l = a + (n-1)d
Substitute values:
50 = 5 + (16-1)d
50 = 5 + 15d
50 - 5 = 15d
15d = 45
d =
d = 3
Hence, common difference = 3.
Answered By
10 Likes
Related Questions
In the given graph ABCD is a parallelogram.
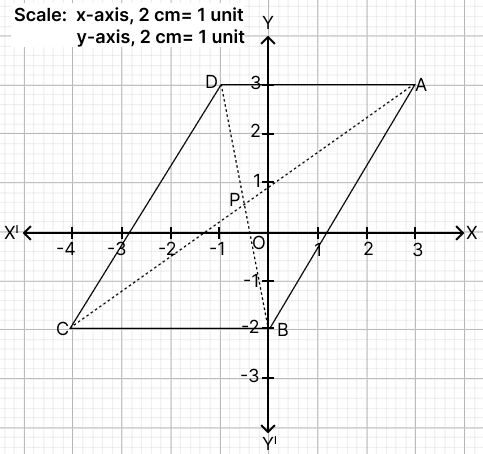
Using the graph, answer the following:
(a) write down the coordinates of A, B, C and D.
(b) calculate the coordinates of ‘P’, the point of intersection of the diagonals AC and BD.
(c) find the slope of sides CB and DA and verify that they represent parallel lines.
(d) find the equation of the diagonal AC.
Solve the following inequation, write the solution set and represent it on the real number line.
Prove that:
Using properties of proportion, find the value of ‘x’: