In the given graph ABCD is a parallelogram.

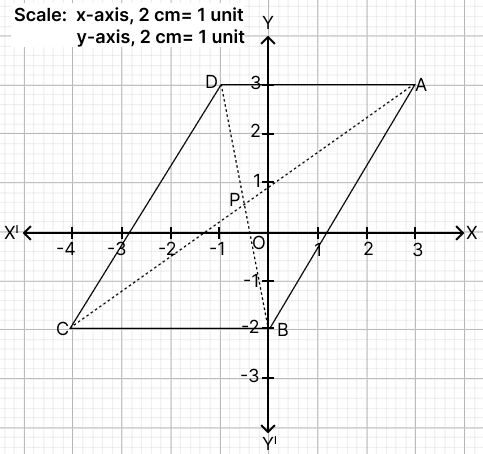
Using the graph, answer the following:

(a) write down the coordinates of A, B, C and D.

(b) calculate the coordinates of ‘P’, the point of intersection of the diagonals AC and BD.

(c) find the slope of sides CB and DA and verify that they represent parallel lines.

(d) find the equation of the diagonal AC.

(a) From graph,

A(3, 3), B(0, −2), C(−4, −2), D(−1, 3).

Hence, A(3, 3), B(0, −2), C(−4, −2), D(−1, 3).

(b) Given,

The diagonals of a parallelogram bisect each other.

Hence, the intersection point P is the midpoint of both AC and BD.

By mid-point formula,

$\Rightarrow M = \Big(\dfrac{x$1+x2}{2}, \dfrac{y1+y2}{2}\Big)

Mid-point of AC :

$\Rightarrow P = \Big(\dfrac{3 + (-4)}{2}\ , \dfrac{3 + (-2)}{2}\Big) \\[1em] \Rightarrow P = \Big(\dfrac{-1}{2}\ , \dfrac{1}{2}\Big) \\[1em] \Rightarrow P = (-0.5, 0.5).$

Hence, P = (-0.5, 0.5).

(c) By formula,

$\text{Slope (m)} = \dfrac{y$2 - y1}{x2 - x1}

Substituting values for line CB,

$\Rightarrow m_{CB} = \dfrac{-2-(-2)}{0-(-4)} \\[1em] = \dfrac{0}{4} \\[1em] = 0.$

Substituting values for line DA,

$\Rightarrow m_{DA} = \dfrac{3-3}{3-(-1)} \\[1em] = \dfrac{0}{4} \\[1em] = 0 .$

Since, slope of parallel lines are equal, thus CB || DA.

Hence, proved that CB || DA.

(d) By formula,

Slope of line = $\dfrac{y$2-y1}{x2-x1}

Slope of AC = $\dfrac{-2 - 3}{-4 - 3} = \dfrac{-5}{-7} = \dfrac{5}{7}$.

Using point-slope formula,

y - y₁ = m(x - x₁)

Equation of AC :

$\Rightarrow y - 3 = \dfrac{5}{7}(x - 3) \\[1em] \Rightarrow 7(y - 3) = 5(x - 3) \\[1em] \Rightarrow 7y - 21 = 5x - 15 \\[1em] \Rightarrow 5x - 7y - 15 + 21 = 0 \\[1em] \Rightarrow 5x - 7y + 6 = 0.$

Hence, equation of the diagonal AC is 5x - 7y + 6 = 0.