Mathematics
In the following figure, AB = AD, AC = AE and ∠BAD = ∠CAE.
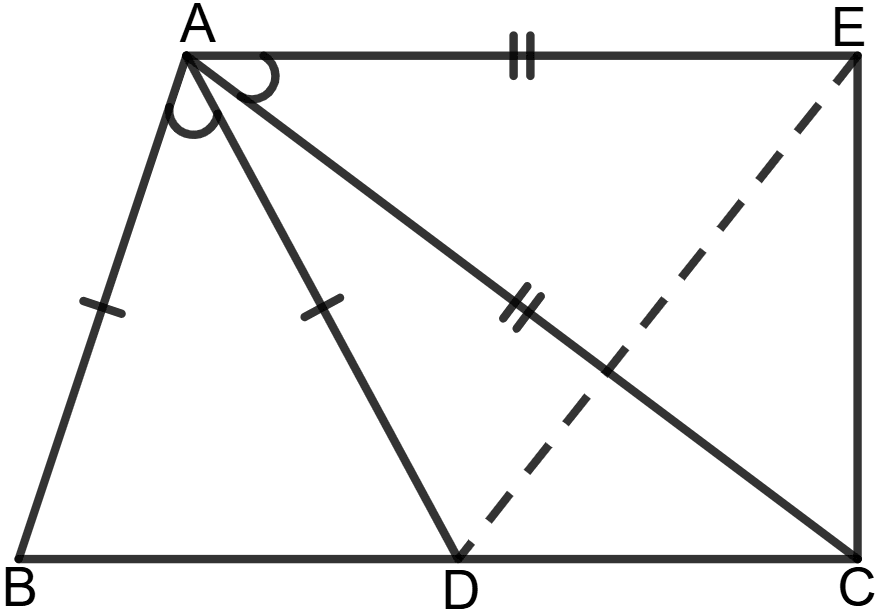
Prove that : BC = ED.
Triangles
5 Likes
Answer
Given: AB = AD, AC = AE and ∠BAD = ∠CAE.
⇒ ∠BAD + ∠DAC = ∠CAE + ∠DAC (Adding ∠DAC on both sides)
⇒ ∠BAC = ∠DAE
In Δ BAC and Δ DAE,
AB = AD (Given)
∠BAC = ∠DAE (Proved above)
AC = AE (Given)
Using SAS congruence criterion,
Δ BAC ≅ Δ DAE
By corresponding parts of congruent triangles,
BC = DE
Hence, BC = DE.
Answered By
2 Likes
Related Questions
In any quadrilateral, the sum of the lengths of its four sides exceeds the sum of the lengths of its diagonals. Prove it.
The side BC of a triangle ABC is produced to D so that CD = AC. If the angle BAD = 109° and the angle ACB = 72°, prove that BD is greater than AD.
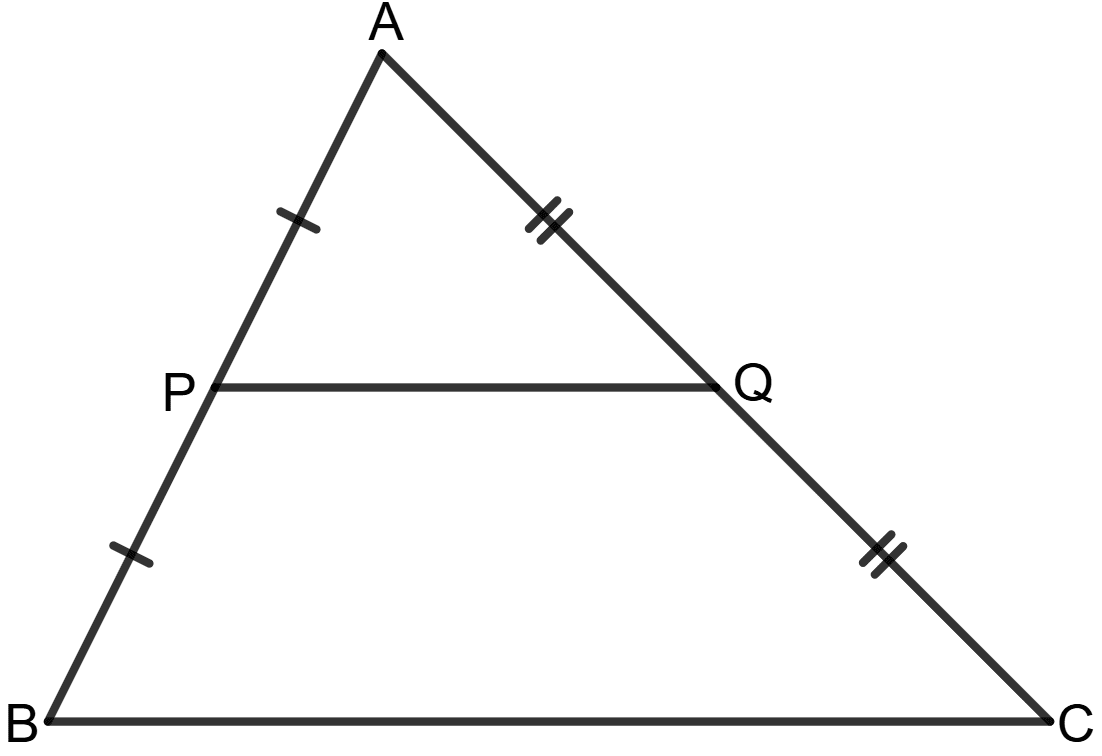
In triangle ABC, P is mid-point of AB and Q is mid-point of AC. If AB = 9.6 cm, BC = 11 cm and AC = 11.2 cm; find the perimeter of the trapezium PBCQ.
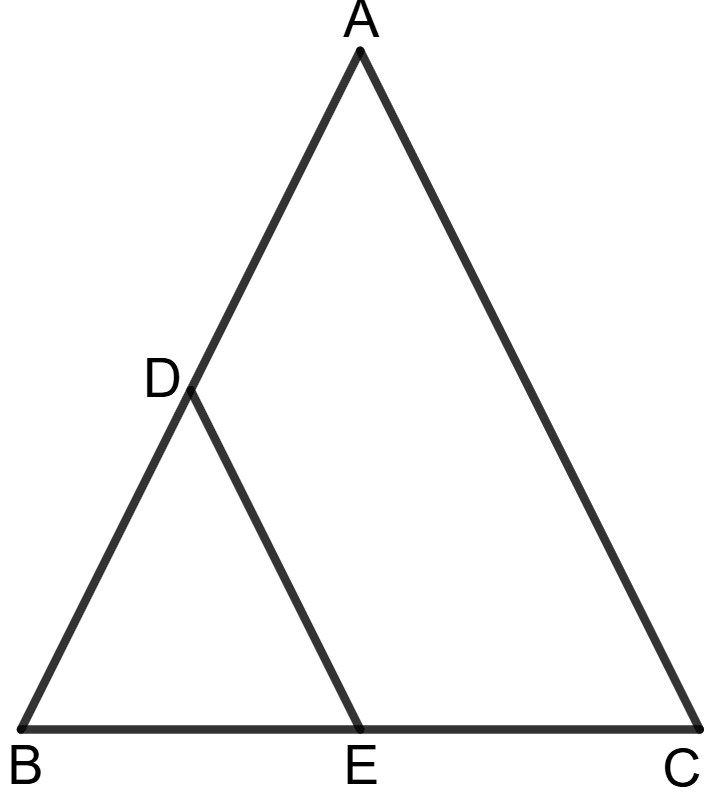
In △ ABC, D is mid-point of AB and E is mid-point of BC. Calculate :
(i) DE, if AC = 6.4 cm,
(ii) ∠DEB, if ∠ACB = 63°.