Mathematics
In any quadrilateral, the sum of the lengths of its four sides exceeds the sum of the lengths of its diagonals. Prove it.
Triangles
2 Likes
Answer
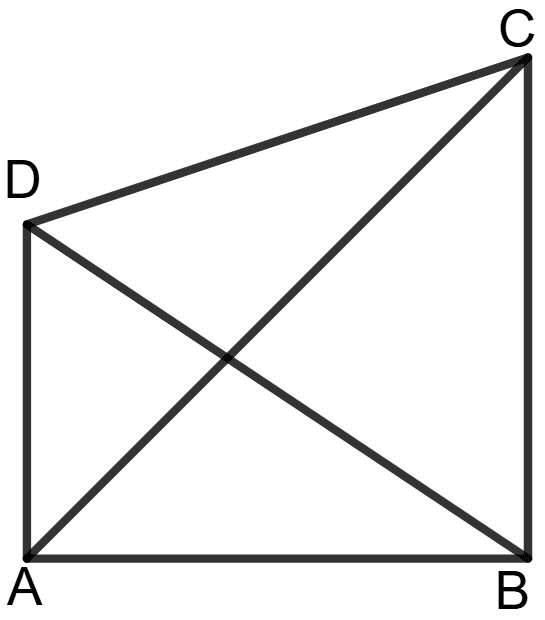
Let ABCD be a quadrilateral.
Construction: Join BD and AC as its diagonals.
To Prove: In any quadrilateral, the sum of the lengths of its four sides is greater than the sum of the lengths of its diagonals.
Proof: Using the Triangle Inequality Theorem, which states that the sum of the lengths of any two sides of a triangle is always greater than the length of the third side:
In Δ ABC:
AB + CB > AC ……………….(1)
Similarly, in Δ BCD:
BC + CD > BD ……………….(2)
Similarly, in Δ CDA:
CD + DA > AC ……………….(3)
Similarly, in Δ DAB:
DA + AB > BD ……………….(4)
Now, adding the inequalities (1) and (2),
(AB + BC) + (BC + CD) > AC + BD
⇒ AB + BC + BC + CD > AC + BD
⇒ AB + 2BC + CD > AC + BD ………………..(5)
Adding the inequalities from (3) and (4),
(CD + DA) + (DA + AB) > AC + BD
⇒ CD + DA + DA + AB > AC + BD
⇒ CD + 2DA + AB > AC + BD ……………….(6)
Adding equations (5) and (6), we get:
⇒ (AB + 2BC + CD) + (CD + 2DA + AB) > (AC + BD) + (AC + BD)
⇒ AB + 2BC + CD + CD + 2DA + AB > 2(AC + BD)
⇒ 2(AB + BC + CD + DA) > 2(AC + BD)
⇒ AB + BC + CD + DA > AC + BD
Hence, the sum of the lengths of the four sides of a quadrilateral is greater than the sum of the lengths of its diagonals.
Answered By
1 Like
Related Questions
In triangle ABC, given below, P is a point inside △ABC.
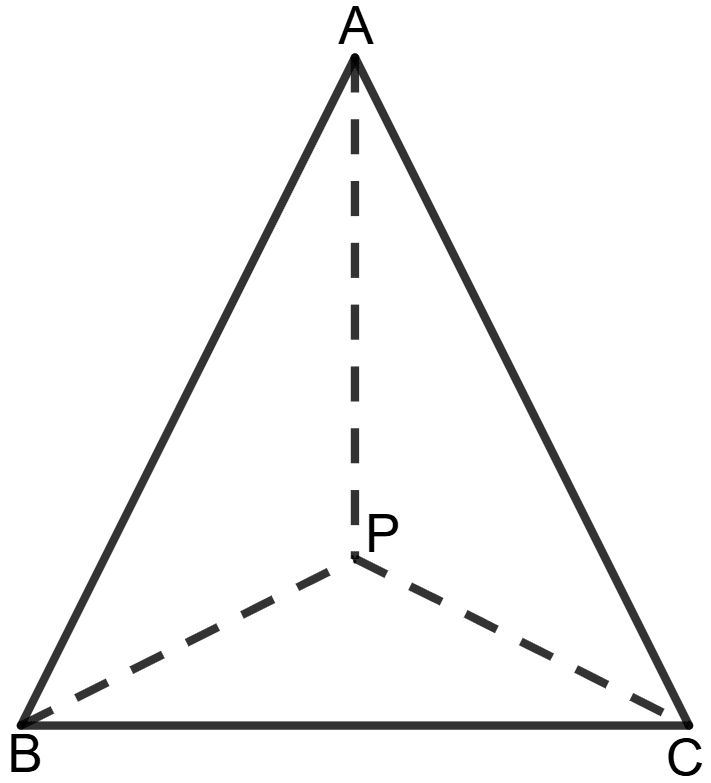
Prove that :
AP + BP + CP > (AB + BC + CA)
Two sides of a triangle are 8 cm and 11 cm, The length of its third side lies between a cm b cm, find the values of a and b if a < b.
The side BC of a triangle ABC is produced to D so that CD = AC. If the angle BAD = 109° and the angle ACB = 72°, prove that BD is greater than AD.
In the following figure, AB = AD, AC = AE and ∠BAD = ∠CAE.
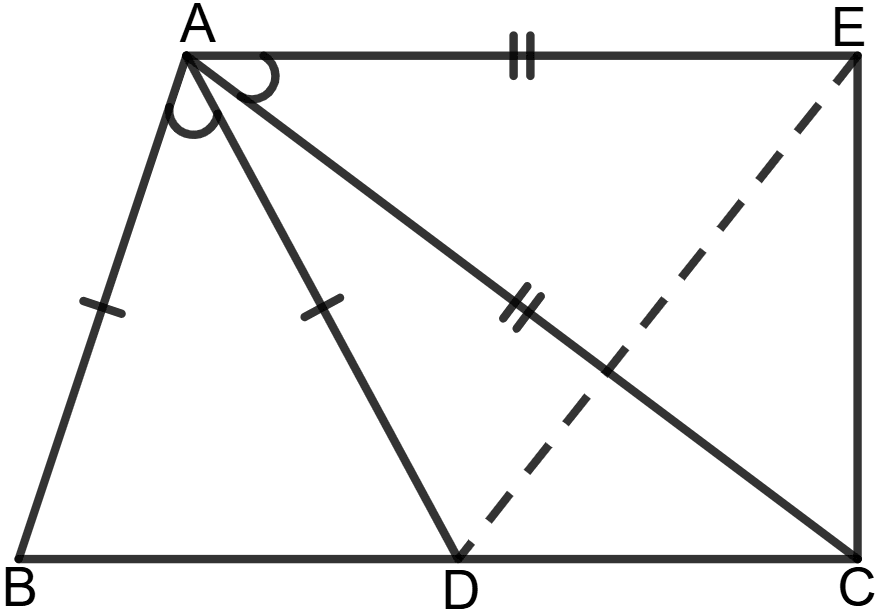
Prove that : BC = ED.