Mathematics
In triangle ABC, given below, P is a point inside △ABC.
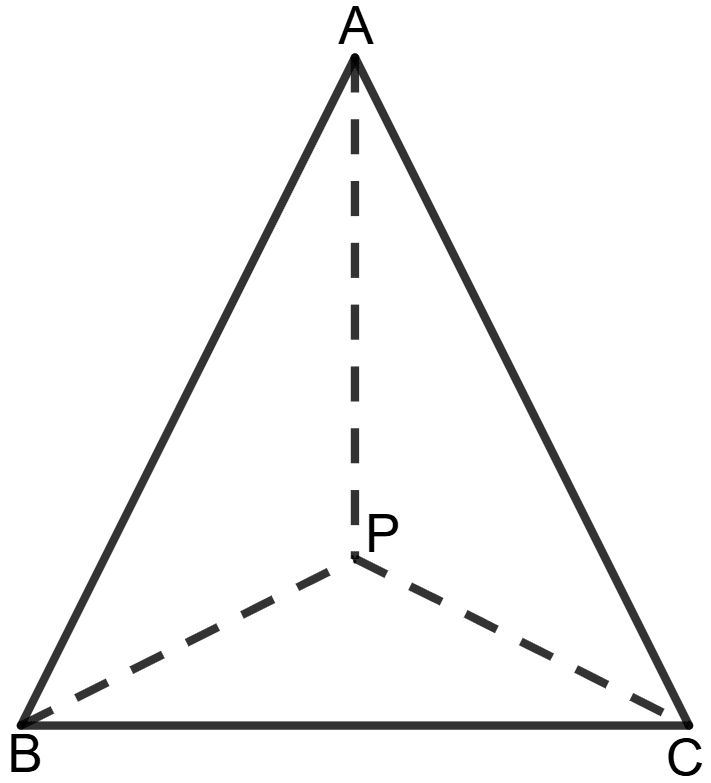
Prove that :
AP + BP + CP > (AB + BC + CA)
Triangles
1 Like
Answer
Given: P is a point inside △ ABC.
To prove: AP + BP + CP > (AB + BC + CA)
Proof: Using the Triangle Inequality Theorem, which states that the sum of the lengths of any two sides of a triangle is greater than the third side:
In Δ PAB:
AP + BP > AB ……………….(1)
Similarly, in Δ PBC:
BP + CP > BC ……………….(2)
Similarly, in Δ PAC:
AP + CP > AC ……………….(3)
Now, adding the equations (1), (2) and (3):
AP + BP + BP + CP + AP + CP > AB + BC + AC
⇒ 2AP + 2BP + 2CP > AB + BC + AC
⇒ 2(AP + BP + CP) > AB + BC + AC
⇒ AP + BP + CP > (AB + BC + AC)
Hence, AP + BP + CP > (AB + BC + AC).
Answered By
2 Likes
Related Questions
ABC is an equilateral triangle. If AD bisects angle A, prove that AD is perpendicular bisector of BC.
In the following figure, AE//BC. Find values of x and y.
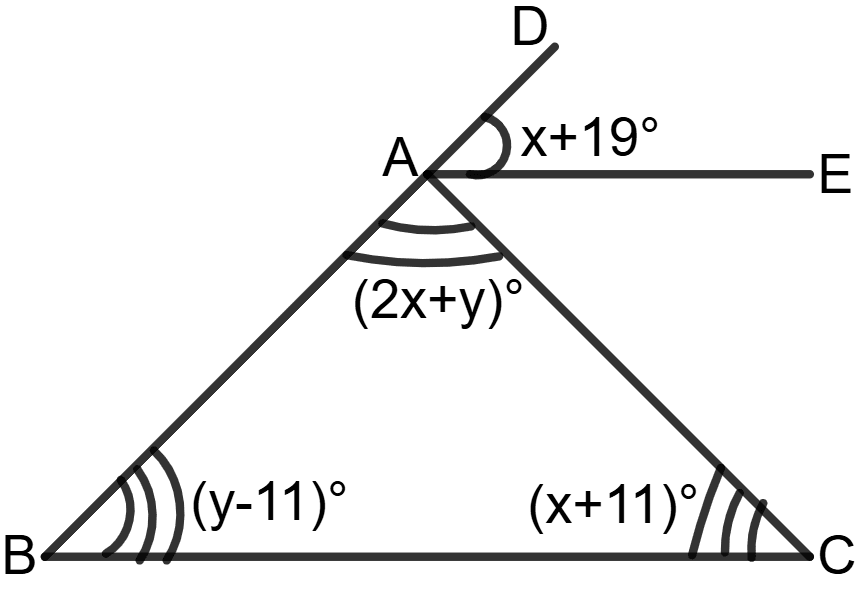
Two sides of a triangle are 8 cm and 11 cm, The length of its third side lies between a cm b cm, find the values of a and b if a < b.
In any quadrilateral, the sum of the lengths of its four sides exceeds the sum of the lengths of its diagonals. Prove it.