Mathematics
Two sides of a triangle are 8 cm and 11 cm, The length of its third side lies between a cm b cm, find the values of a and b if a < b.
Triangles
6 Likes
Answer
Using the Triangle Inequality Theorem, which states:
The sum of any two sides of a triangle is greater than the third side:
Third side < 11 + 8 = 19 cm
The difference between any two sides of a triangle is less than the third side:
Third side > 11 - 8 = 3 cm
Thus, the length of the third side must lie between 3 cm and 19 cm.
Given that a < b, we have: a = 3 cm and b = 19 cm
Hence, a = 3 cm and b = 19 cm.
Answered By
2 Likes
Related Questions
In the following figure, AE//BC. Find values of x and y.
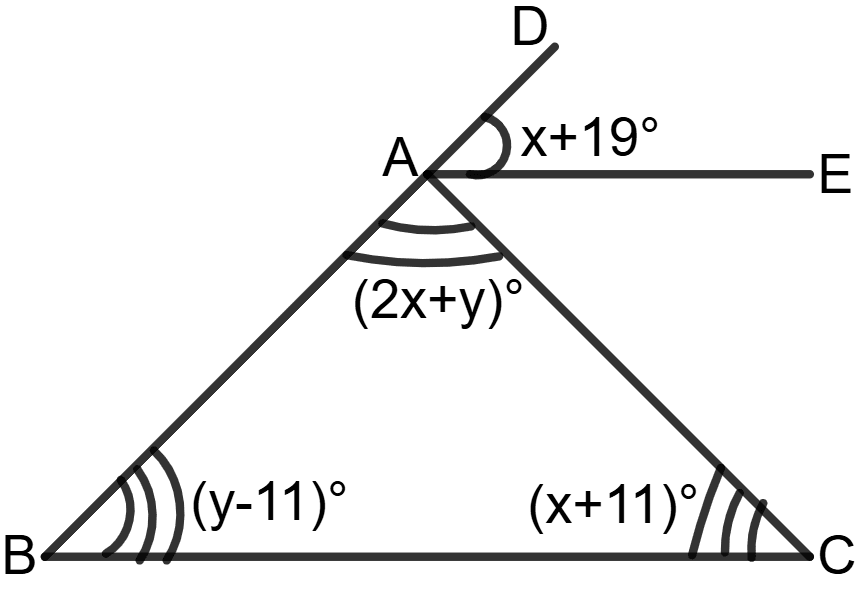
In triangle ABC, given below, P is a point inside △ABC.
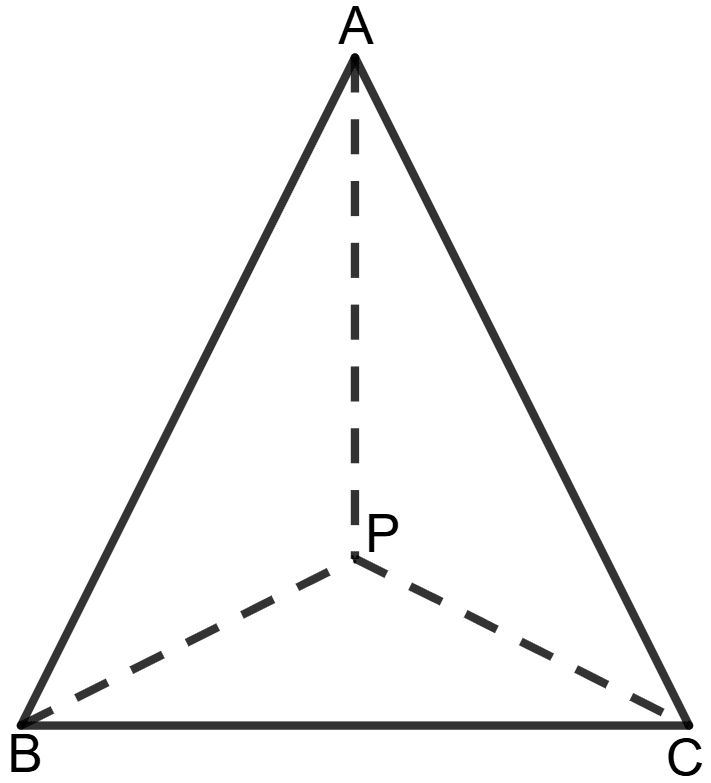
Prove that :
AP + BP + CP > (AB + BC + CA)
In any quadrilateral, the sum of the lengths of its four sides exceeds the sum of the lengths of its diagonals. Prove it.
The side BC of a triangle ABC is produced to D so that CD = AC. If the angle BAD = 109° and the angle ACB = 72°, prove that BD is greater than AD.