Mathematics
The side BC of a triangle ABC is produced to D so that CD = AC. If the angle BAD = 109° and the angle ACB = 72°, prove that BD is greater than AD.
Triangles
3 Likes
Answer
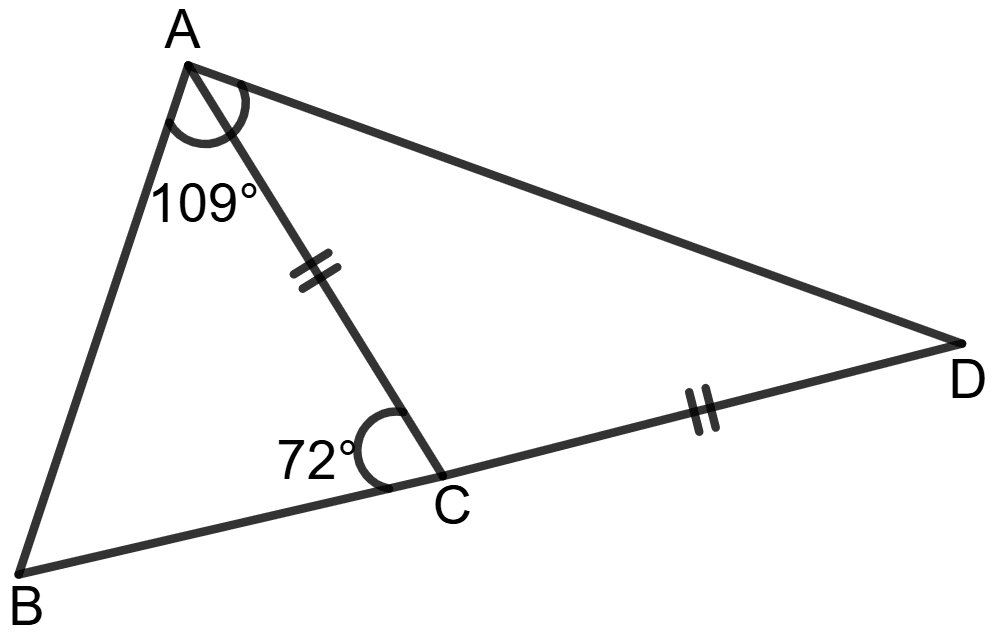
Given: ∠BAD = 109°, ∠ACB = 72° and CD = AC (i.e., Δ ACD is isosceles).
∠BCA + ∠ACD = 180° (∴ Linear pair)
⇒ 72° + ∠ACD = 180°
⇒ ∠ACD = 180° - 72°
⇒ ∠ACD = 108°
Since AC = CD, Δ ACD is isosceles. So:
⇒ ∠ADC = ∠CAD
Using the angle sum property in Δ ACD;
∠ACD + ∠ADC + ∠CAD = 180°
⇒ 108° + ∠ADC + ∠CAD = 180°
⇒ 2∠ADC = 180° - 108°
⇒ 2∠ADC = 72°
⇒ ∠ADC = = 36° and ∠CAD = 36°
From the figure, ∠BAD = ∠BAC + ∠CAD
⇒ 109° = ∠BAC + 36°
⇒ ∠BAC = 109° - 36° = 73°
In Δ ABC,
∠ABC + ∠ACB + ∠CAB = 180°
⇒ ∠ABC + 72° + 73° = 180°
⇒ ∠ABC + 145° = 180°
⇒ ∠ABC = 180° - 145°
⇒ ∠ABC = 35°
In Δ ABD, the angles are ∠A = 109°, ∠B = 35° and ∠D = 36°.
Since larger angles correspond to larger sides, we observe:
∠A > ∠D > ∠B
So, the corresponding sides follow:
⇒ BD > AB > AD
Hence, BD is greater than AD.
Answered By
1 Like
Related Questions
Two sides of a triangle are 8 cm and 11 cm, The length of its third side lies between a cm b cm, find the values of a and b if a < b.
In any quadrilateral, the sum of the lengths of its four sides exceeds the sum of the lengths of its diagonals. Prove it.
In the following figure, AB = AD, AC = AE and ∠BAD = ∠CAE.
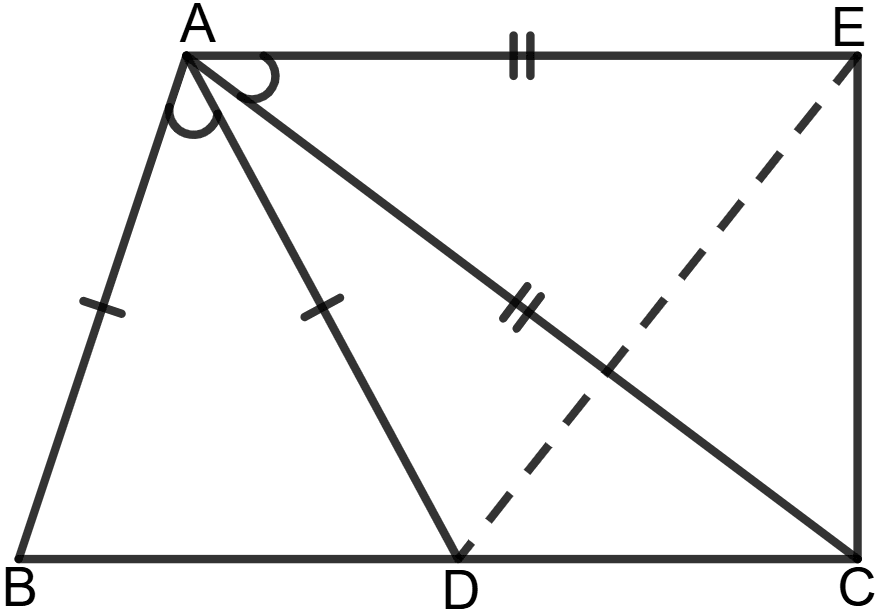
Prove that : BC = ED.
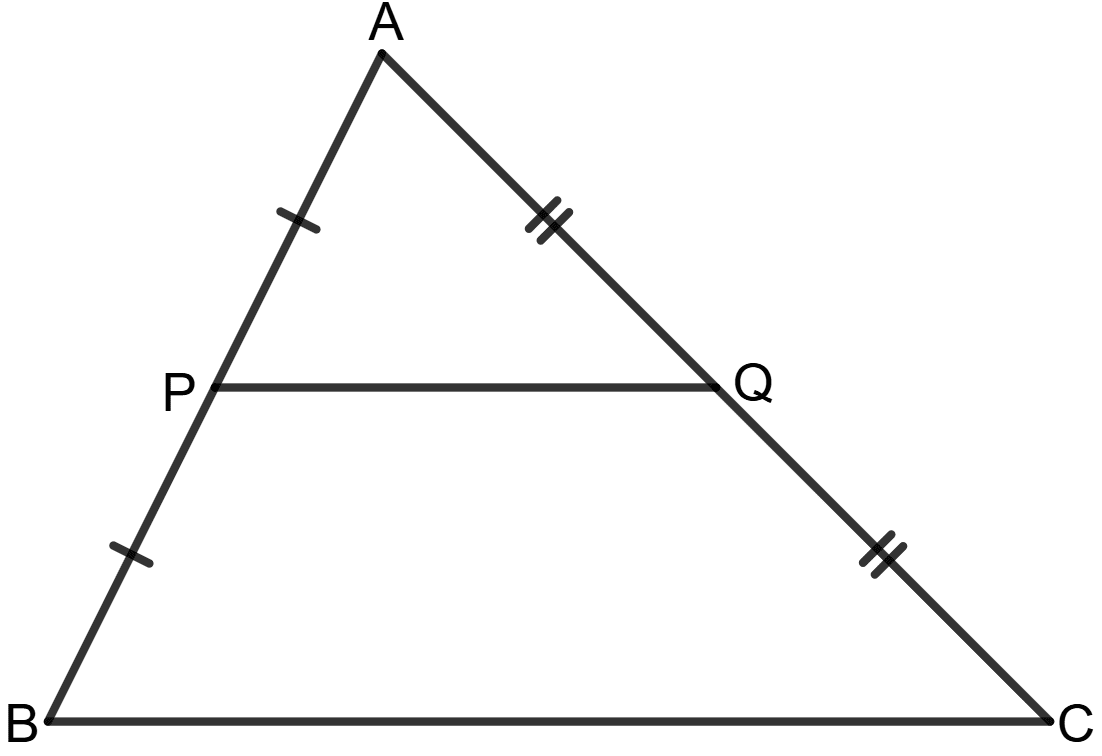
In triangle ABC, P is mid-point of AB and Q is mid-point of AC. If AB = 9.6 cm, BC = 11 cm and AC = 11.2 cm; find the perimeter of the trapezium PBCQ.