Mathematics
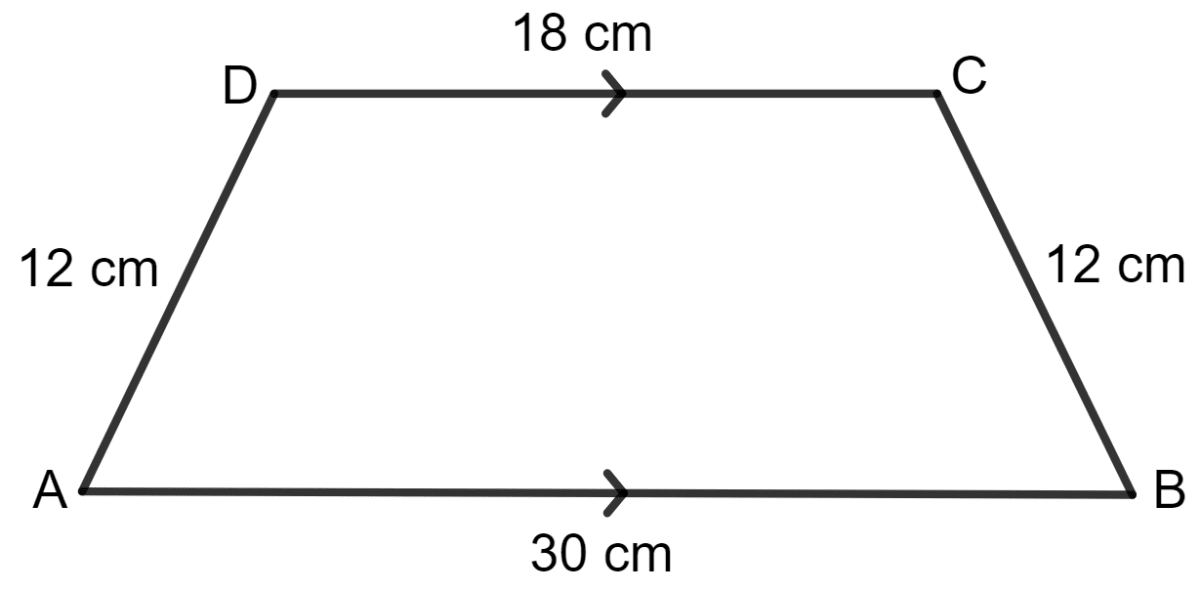
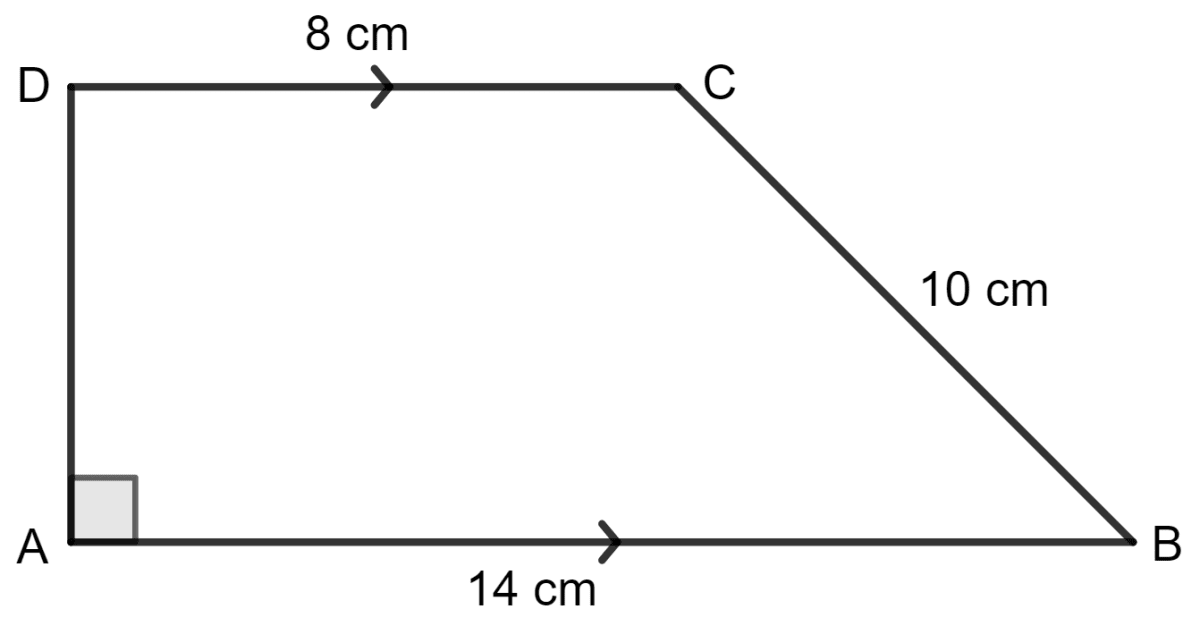
For the trapezium given below; find its area.
Mensuration
5 Likes
Answer
Draw CO such that CO is perpendicular to AB.
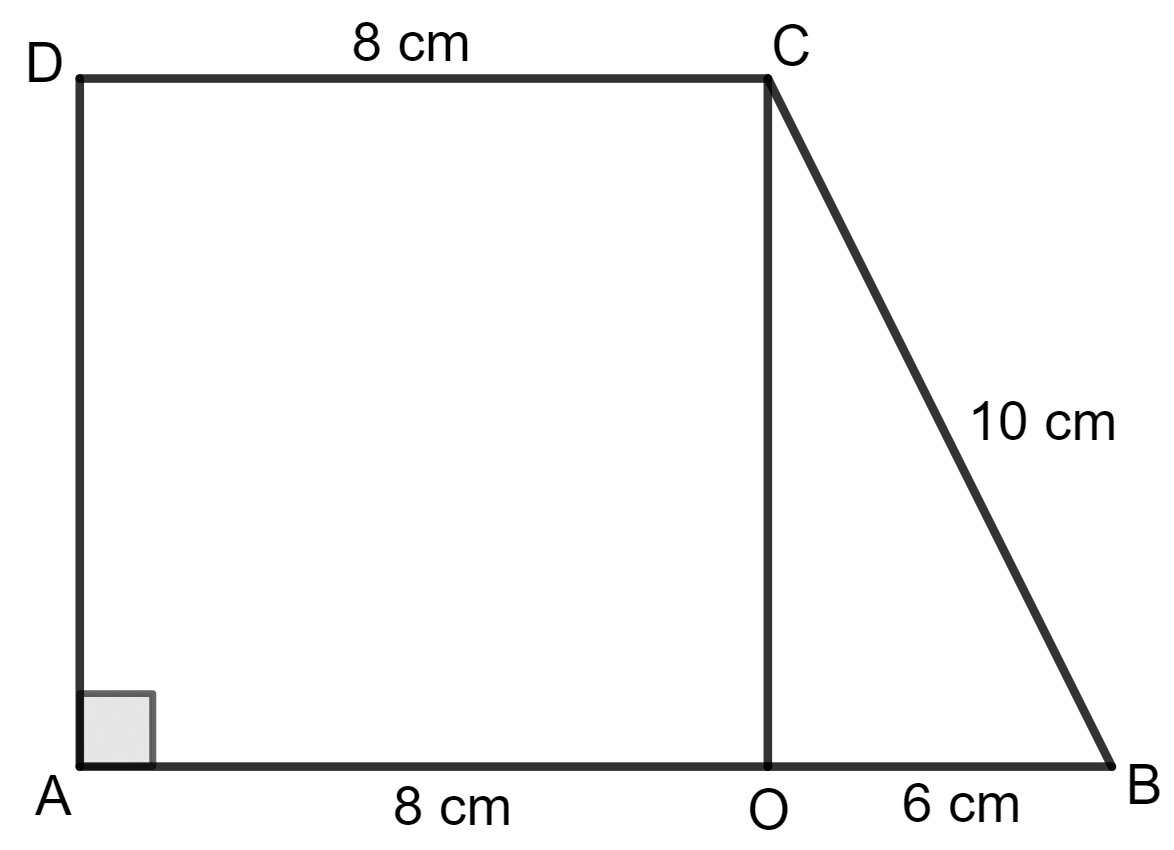
AO = DC = 8 cm
AB = AO + OB
⇒ 14 = 8 + OB
⇒ OB = 14 - 8 = 6 cm
Area of trapezium ABCD = x (sum of parallel sides) x height
In triangle BCO, by using the Pythagoras theorem,
Base2 + Height2 = Hypotenuse2
⇒ (6)2 + Height2 = 102
⇒ 36 + Height2 = 100
⇒ Height2 = 100 - 36
⇒ Height2 = 64
⇒ Height =
⇒ Height = 8 cm
Area of trapezium ABCD = x (8 + 14) x 8
= x 22 x 8 sq. cm
= 11 x 8 sq. cm
= 88 sq. cm
Hence, the area of trapezium ABCD is 88 sq. cm.
Answered By
2 Likes
Related Questions
A wire when bent in the form of a square encloses an area of 484 m2. Find the largest area enclosed by the same wire when bent to form :
(i) an equilateral triangle.
(ii) a rectangle of breadth 16 m.
For the trapezium given below; find its area.
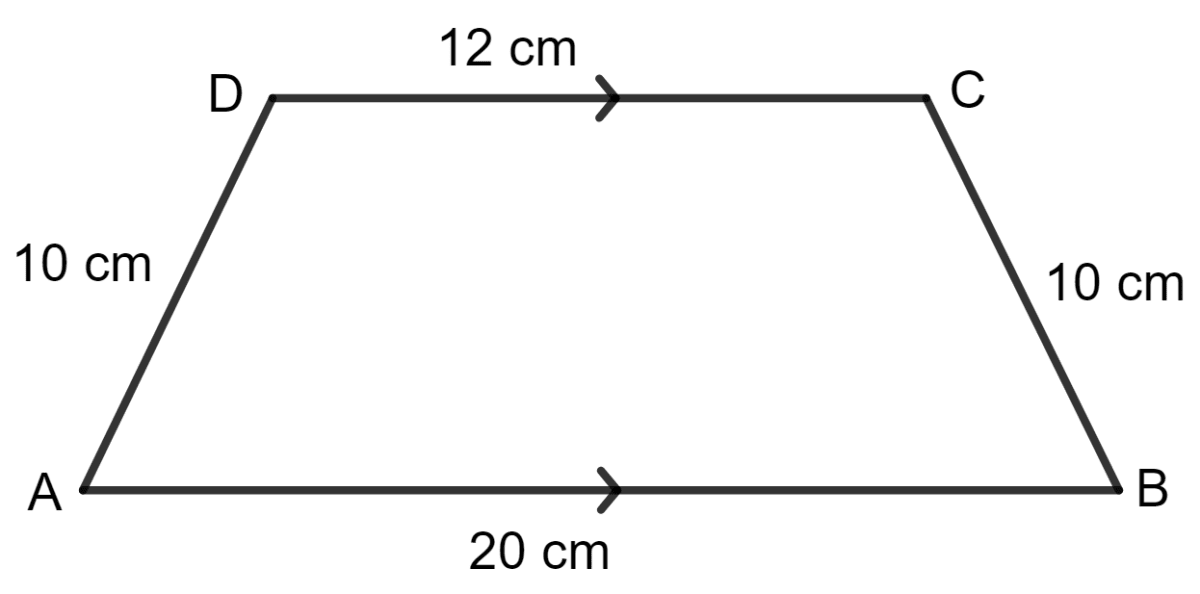
For the trapezium given below; find its area.
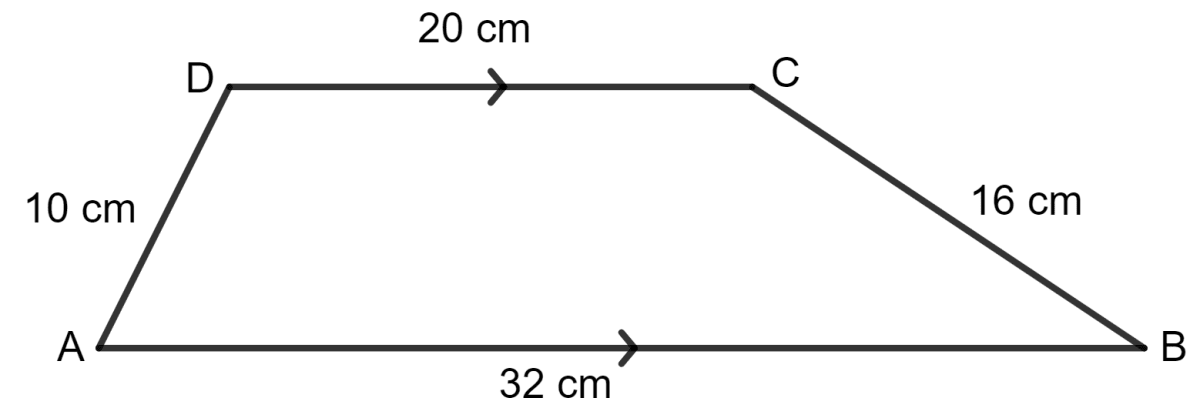
For the trapezium given below; find its area.