Mathematics
For the trapezium given below; find its area.
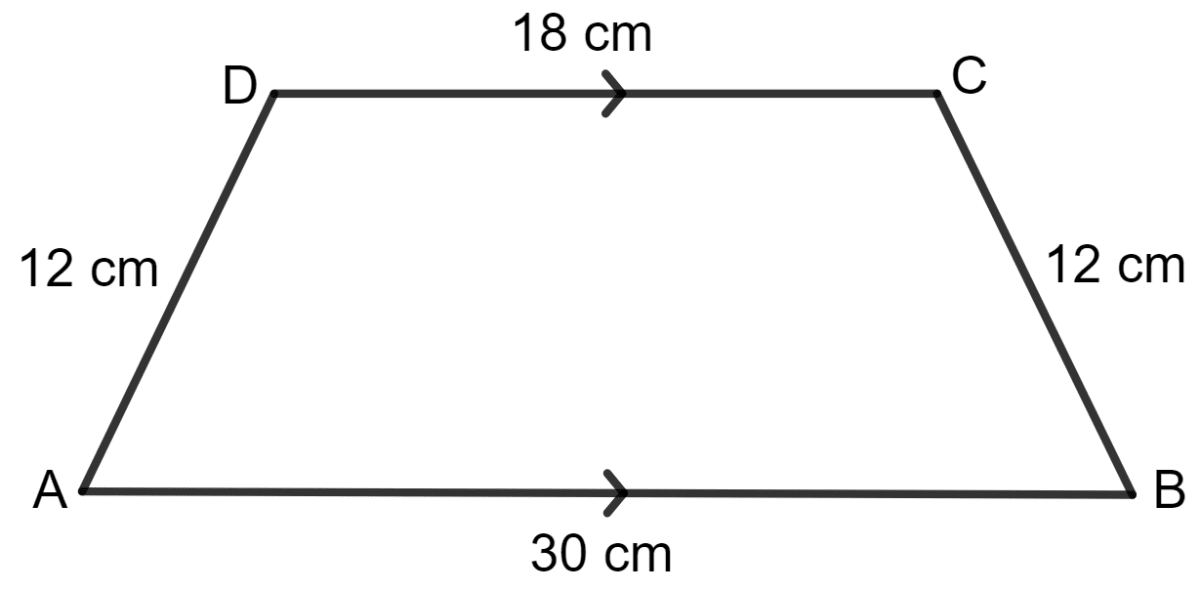
Mensuration
3 Likes
Answer
Draw DE and CF perpendicular to AB.
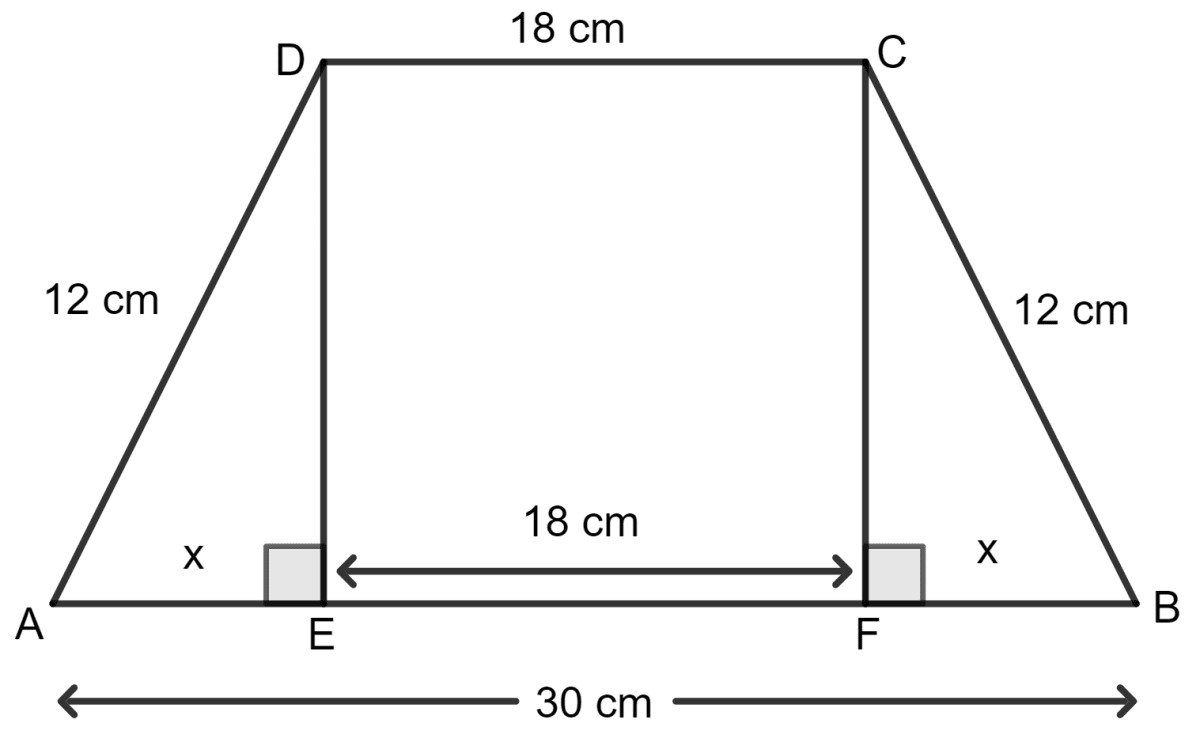
ABCD is an isosceles trapezium.
Let EF = FB = x cm
DC = EF = 18 cm
AB = AE + EF + FB
⇒ 30 = x + 18 + x
⇒ 30 = 2x + 18
⇒ 2x = 30 - 18
⇒ 2x = 12
⇒ x =
⇒ x = 6 cm
As EDA is a right angled triangle, by using the Pythagoras theorem,
Base2 + Height2 = Hypotenuse2
⇒ (6)2 + height2 = 122
⇒ 36 + height2 = 144
⇒ height2 = 144 - 36
⇒ height2 = 108 cm
⇒ height = cm
⇒ height = 10.39 cm
Area of trapezium ABCD = x (sum of parallel sides) x height
= x (18 + 30) x 10.39
= x 48 x 10.39 sq. cm
= 24 x 10.39 sq. cm
= 249.41 sq. cm
Hence, the area of trapezium ABCD is 249.41 sq. cm.
Answered By
1 Like
Related Questions
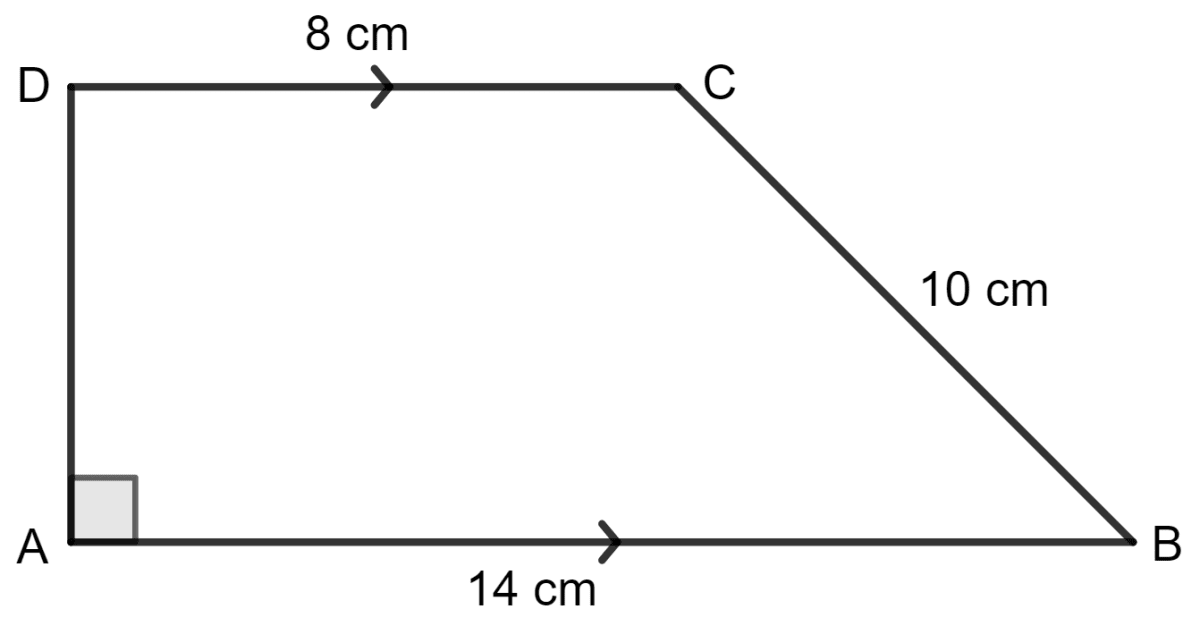
For the trapezium given below; find its area.
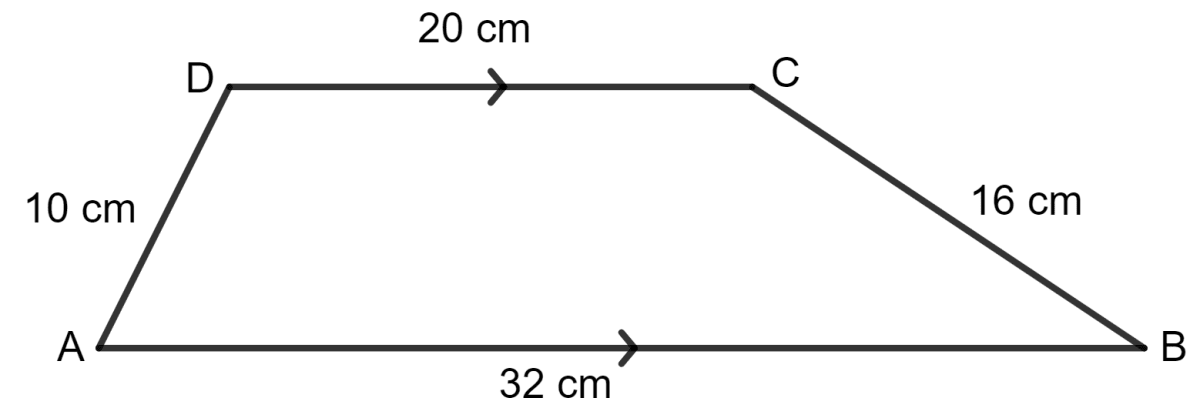
For the trapezium given below; find its area.
The perimeter of a rectangular board is 70 cm. Taking its length as x cm, find its width in terms of x.
If the area of the rectangular board is 300 cm2; find its dimensions.
The area of a rectangle is 640 m2. Taking its length as x m; find, in terms of x, the width of the rectangle. If the perimeter of the rectangle is 104 m; find its dimensions.