Given below are the angles x and y.

Without measuring these angles, construct :

(i) ∠ABC = x + y

(ii) ∠ABC = 2x + y

(iii) ∠ABC = x + 2y

(i) Steps:

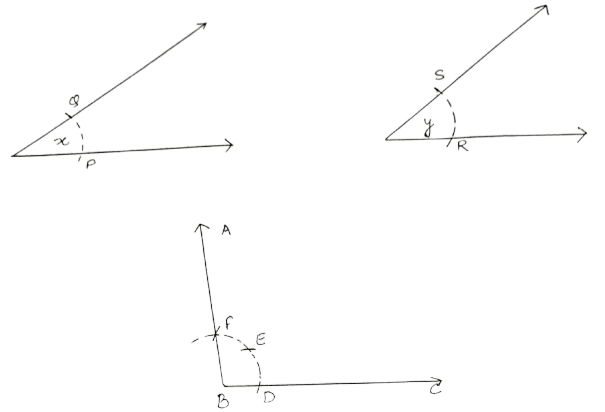
As shown above:

1. Draw line segment BC of any suitable length.

2. With B as centre, draw an arc of any suitable radius. With the same radius, draw arcs with the vertices of given angles as centres. Let these arcs cut arms of the angle x at the points P and Q, and arms of the angle y at points R and S.

3. From the arc, with centre B, cut DE = PQ = x and EF = SR = y.

4. Join BF and produce upto point A.

Hence, ∠ ABC = x + y.

(ii) Steps:

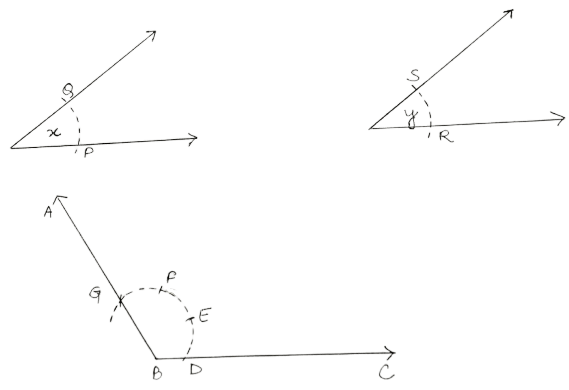
As shown above:

1. Draw line segment BC of any suitable length.

2. With B as centre, draw an arc of any suitable radius. With the same radius, draw arcs with the vertices of given angles as centres. Let these arcs cut arms of the angle x at the points P and Q, and arms of the angle y at the points R and S.

3. From the arc, with centre B, cut DE = PQ = x, EF = PQ = x and FG = RS = y.

4. Join BG and produce upto point A.

Hence, ∠ ABC = x + x + y = 2x + y.

(iii) Steps:

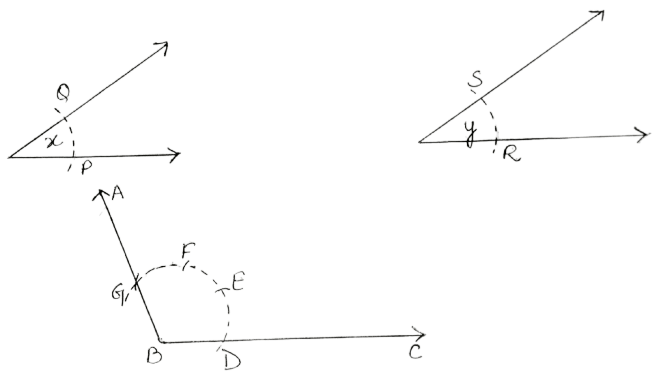
As shown above:

1. Draw line segment BC of any suitable length.

2. With B as centre, draw an arc of any suitable radius. With the same radius, draw arcs with the vertices of given angles as centres. Let these arcs cut arms of the angle x at the points P and Q, and arms of the angle y at the points R and S.

3. From the arc, with centre B, cut DE = PQ = x, EF = RS = y and FG = RS = y.

4. Join BG and produce upto point A.

Hence, ∠ ABC = x + y + y = x + 2y.