In each of the following, draw a perpendicular through point P to the line segment AB :

(i)

(ii)

(iii)

(i) Steps:

1. With P as center, draw an arc of a suitable radius which cuts AB at points C and D.

2. With C and D as centers, draw arcs of equal radii and let these arcs intersect each other at point Q.

(The radius of these arcs must be more than half of CD and both the arcs must be drawn on the other side.)

3. Join P and Q.

4. Let PQ cut AB at point O.

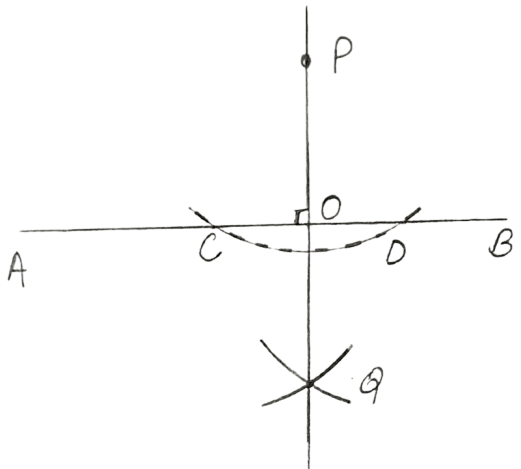
Clearly, ∠AOP = ∠BOP = 90°

Hence, OP is the required perpendicular.

(ii) Steps:

1. With P as center, draw an arc with a suitable radius which cuts AB at points C and D.

2. Taking C and D as centers, draw arcs of equal radii which cut each other at point O.

(The radius must be more than half the distance between C and D.)

3. Join P and O.

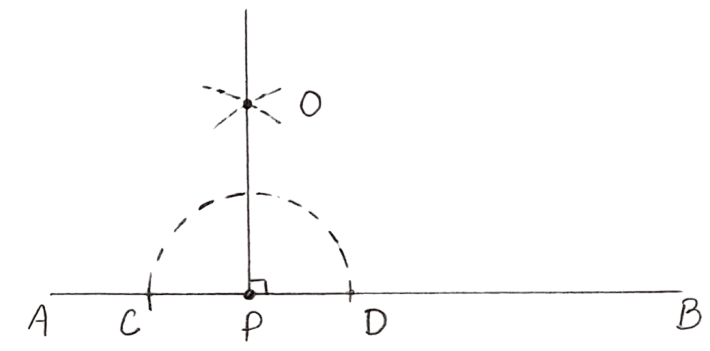
So, ∠OPA = ∠OPB = 90°.

Hence, OP is the required perpendicular.

(iii) Steps:

1. With P as center, draw an arc of a suitable radius which cuts AB at points C and D.

2. With C and D as centers, draw arcs of equal radii and let these arcs intersect each other at point Q.

(The radius of these arcs must be more than half of CD and both the arcs must be drawn on the other side.)

3. Join P and Q.

4. Let PQ cut AB at point O.

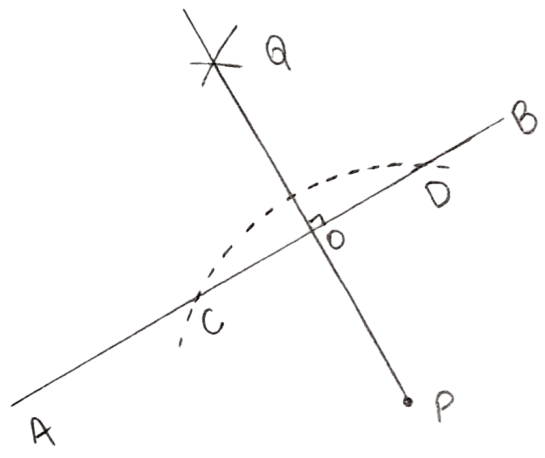
Clearly, ∠AOP = ∠BOP = 90°

Hence, OP is the required perpendicular.