In the given figure, AB and EC are parallel to each other. Sides AD and BC are 2 cm each and are perpendicular to AB.

Given that ∠AED = 60° and ∠ACD = 45°; calculate :

(i) AB

(ii) AC

(iii) AE

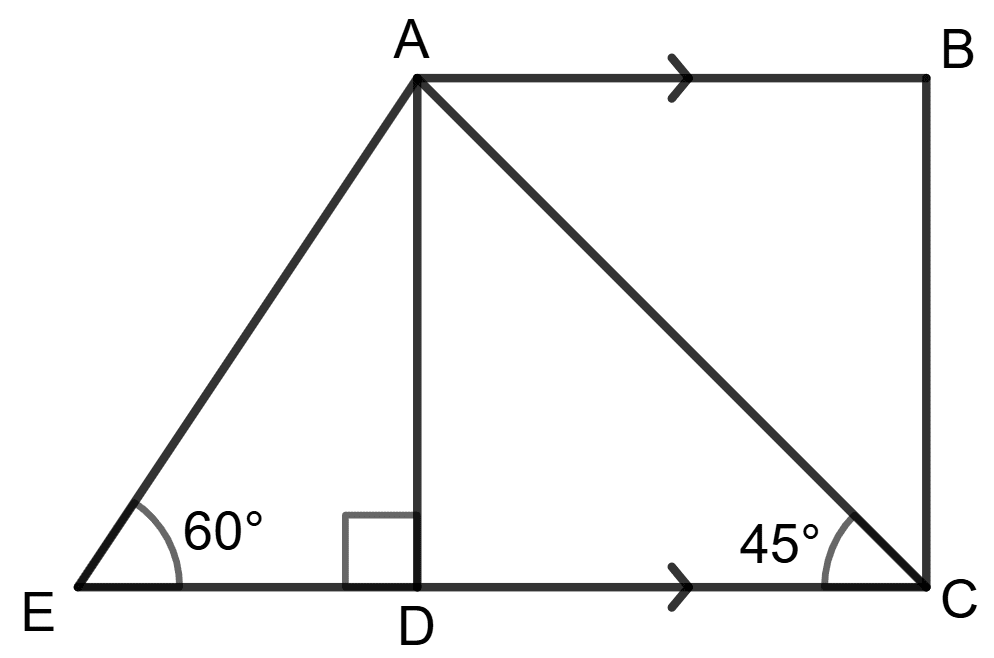
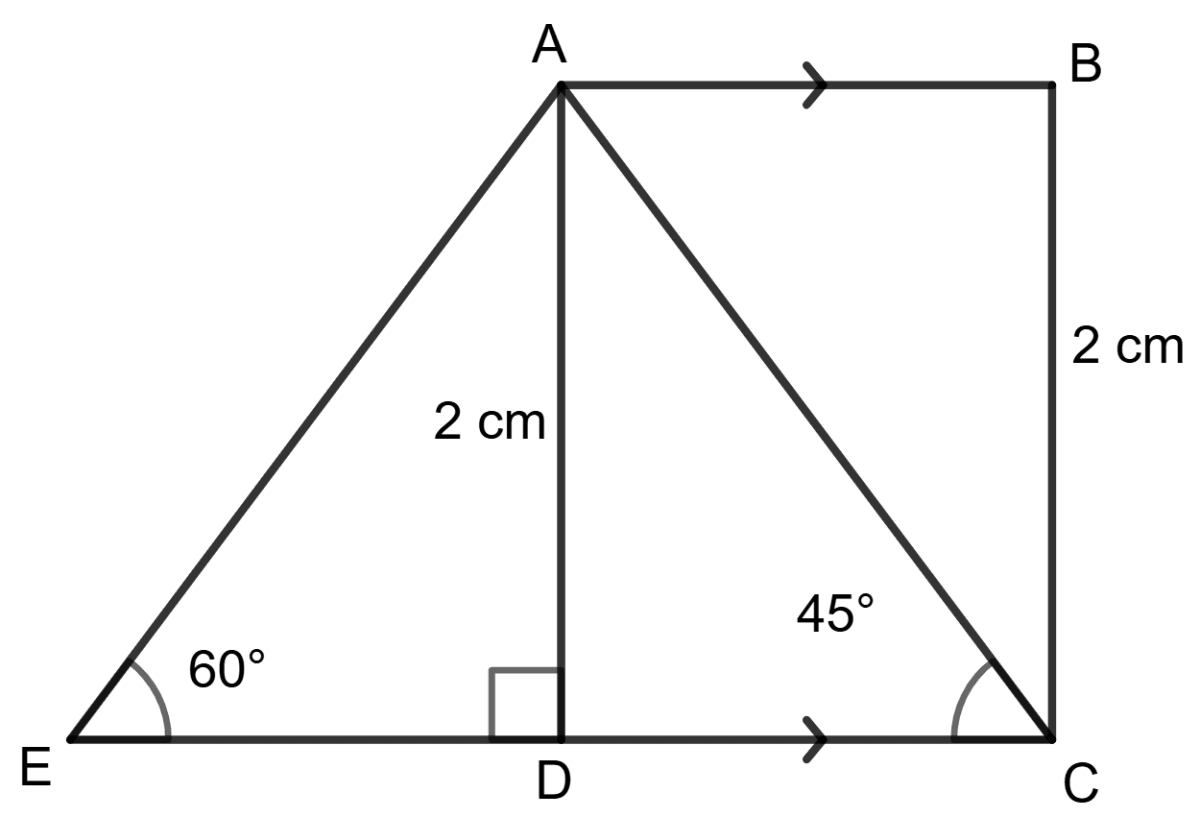
(i) In Δ ADC,

$\text{tan 45°} = \dfrac{Perpendicular}{Base}\\[1em] ⇒ 1 = \dfrac{AD}{DC}\\[1em] ⇒ 1 = \dfrac{2}{DC}\\[1em] ⇒ DC = 2$

DC = AB = 2 cm

Hence, AB = 2 cm.

(ii) In Δ ADC,

$\text{sin 45°} = \dfrac{Perpendicular}{Hypotenuse}\\[1em] ⇒ \dfrac{1}{\sqrt2} = \dfrac{AD}{AC}\\[1em] ⇒ \dfrac{1}{\sqrt2} = \dfrac{2}{AC}\\[1em] ⇒ AC = 2\sqrt2 = 2.83 cm$

Hence, AC = 2.83 cm.

(iii) In Δ ADE,

$\text{sin 60°} = \dfrac{Perpendicular}{Hypotenuse}\\[1em] ⇒ \dfrac{\sqrt3}{2} = \dfrac{AD}{AE}\\[1em] ⇒ \dfrac{\sqrt3}{2} = \dfrac{2}{AE}\\[1em] ⇒ AE = \dfrac{4}{\sqrt3} = 2.31 cm$

Hence, AC = 2.31 cm.