Mathematics
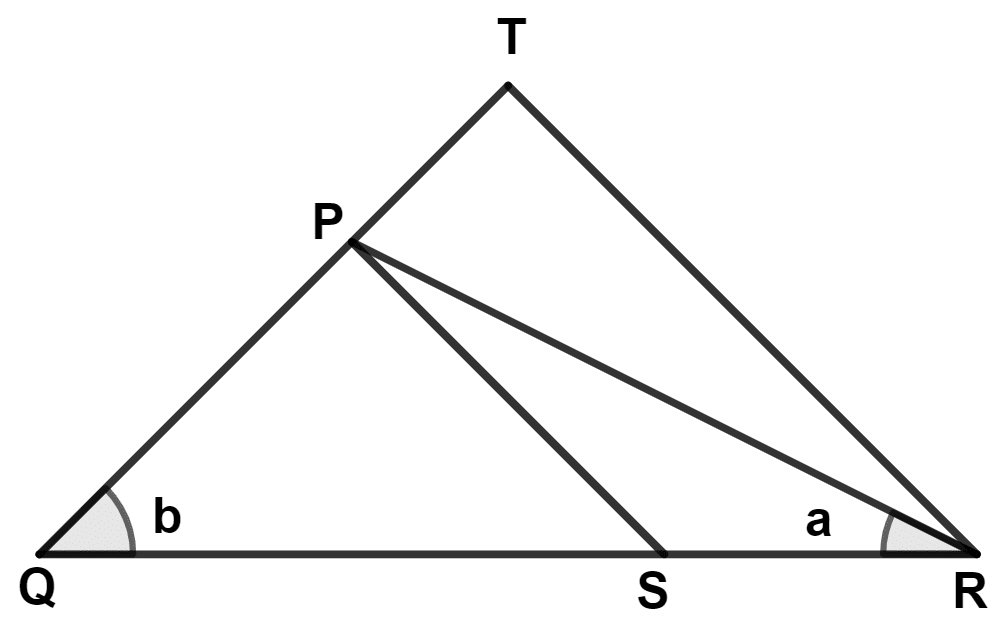
In the given figure, and ∠a = ∠b; show that △ PQS ~ △ TQR.
Similarity
12 Likes
Answer
In Δ PQR,
⇒ ∠a = ∠b (Given)
⇒ PR = PQ (In a triangle sides opposite to equal angles are equal)
Given,
In Δ PQS and Δ TQR
⇒ ∠PQS = ∠TQR = ∠b (Same angle)
⇒ …… [From (1)]
⇒ Δ PQS ~ Δ TQR (By S.A.S. axiom)
Hence, proved that Δ PQS ~ Δ TQR.
Answered By
4 Likes
Related Questions
Let matrix A = , find matrix M so that AM = B.
Find the nature of the roots of the quadratic equation 3x2 - 7x + = 0. If real roots exist, find them.
The mean of the following distribution is 50 and the frequency of the class-interval 20-40 is m, find the value of m.
Class-interval Frequency 0-20 17 20-40 m 40-60 32 60-80 24 80-100 19 The following table shows the marked price, the discount, the number of items and GST rates for two items A and B.
Items Marked price Discount No. of items GST A ₹ 1000 10% 2 0% B ₹ 2000 20% 1 5% Find the total of the money for the above statement.