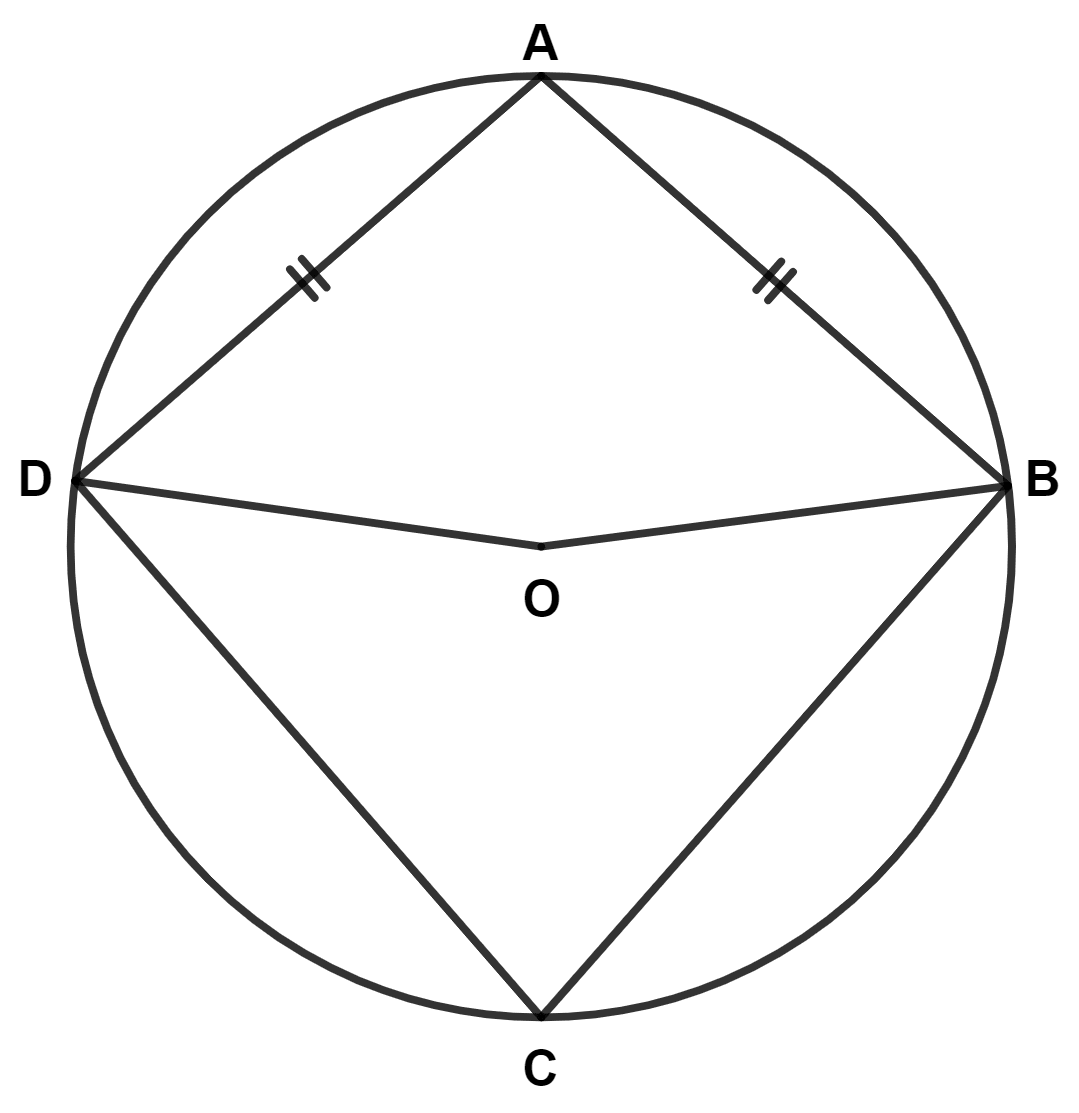
In the given figure, ∠BCD = 75°, O is center of the circle and chord AB = chord AD. Find :

(i) ∠BOD

(ii) ∠ODB

(iii) ∠BAO

(i) We know that,

The angle subtended by an arc of a circle at its center is twice the angle it subtends anywhere on the circle's circumference.

∴ ∠BOD = 2∠BCD

⇒ ∠BOD = 2 × 75° = 150°.

Hence, ∠BOD = 150°.

(ii) Join BD.

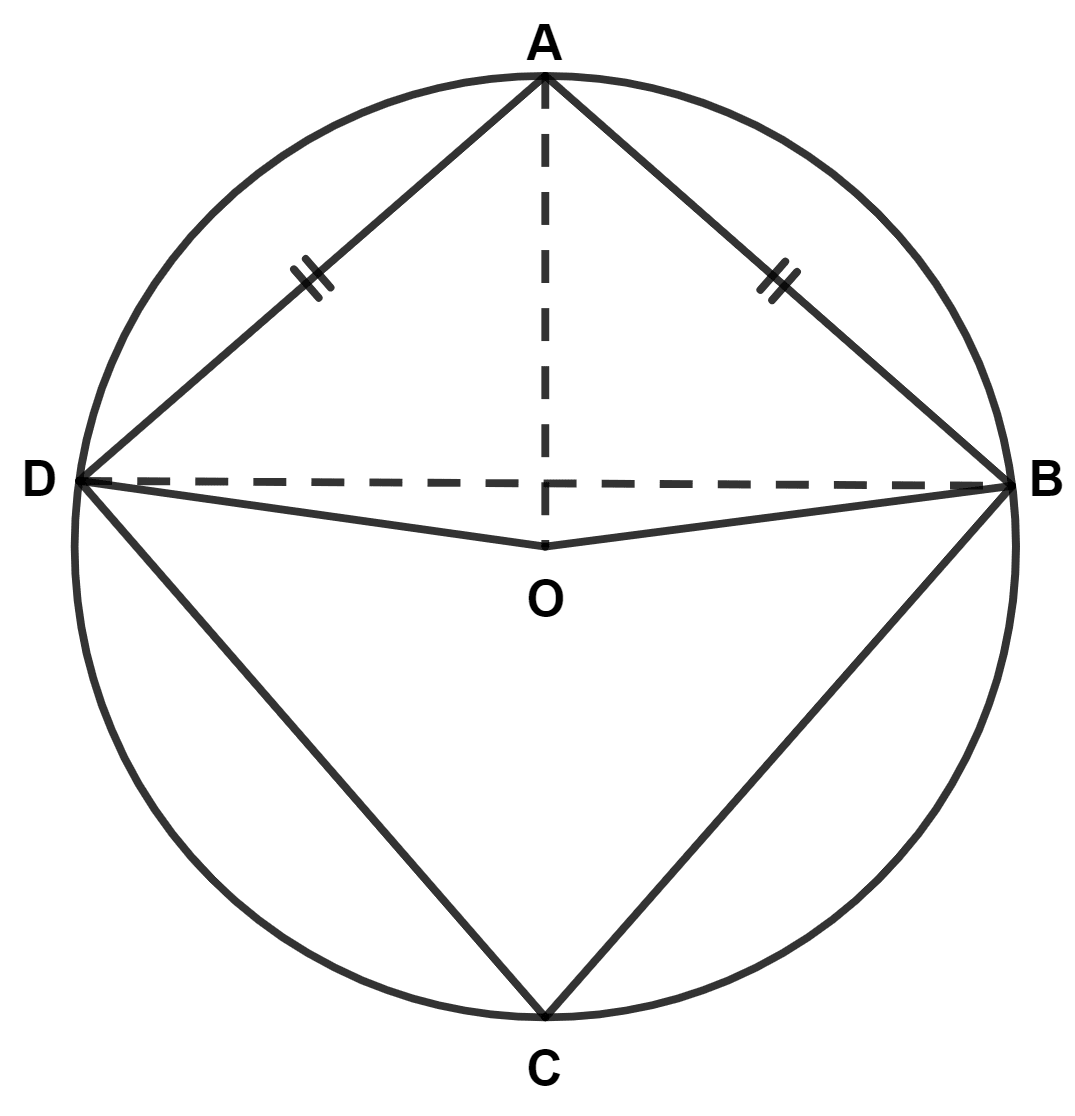
In △ BOD,

⇒ OD = OB (Both equal to radius of circle)

⇒ ∠ODB = ∠OBD = x (let) (Angles opposite to equal sides are equal)

⇒ ∠BOD + ∠ODB + ∠OBD = 180° (By angle sum property)

⇒ 150° + x + x = 180°

⇒ 2x = 180° - 150°

⇒ 2x = 30°

⇒ x = $\dfrac{30°}{2}$ = 15°.

Hence, ∠ODB = 15°.

(iii) Join OA.

As equal chords of a circle subtend equal angles at the center and chord AB = chord AD, so ∠BOA = ∠DOA = a (let).

From figure,

⇒ ∠BOD = ∠BOA + ∠DOA

⇒ 150° = a + a

⇒ 150° = 2a

⇒ a = $\dfrac{150°}{2}$ = 75°

⇒ ∠BOA = 75°.

In cyclic quadrilateral ABCD,

⇒ ∠BAD + ∠BCD = 180°

⇒ ∠BAD + 75° = 180°

⇒ ∠BAD = 180° - 75° = 105°.

In △ BAD,

⇒ ∠BDA = ∠DBA = b (let) (Angles opposite to equal sides are equal)

By angle sum property,

⇒ ∠BAD + ∠BDA + ∠DBA = 180°

⇒ 105° + b + b = 180°

⇒ 2b = 180° - 105°

⇒ 2b = 75°

⇒ b = $\dfrac{75°}{2}$ = 37.5°

From figure,

⇒ ∠OBA = ∠OBD + ∠DBA = ∠OBD + b = 15° + 37.5° = 52.5°

In △ BAO,

⇒ OA = OB (Radius of same circle)

⇒ ∠BAO = ∠OBA = 52.5° (Angles opposite to equal sides are equal)

Hence, the value of ∠BAO = 52.5°.