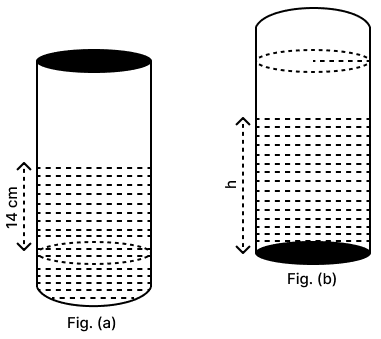
The given figure (fig a) shows a closed liquid container with a cylindrical part and a hemispherical part. It contains liquid upto a height of 14 cm of the cylindrical part. Now this container is inverted as shown in the figure (b), find the height upto which the liquid in figure (b) will stand.

Given, radius of the cylinder is 6 cm and π = $3\dfrac{1}{7}$

In figure (a)

Radius of cylinder = Radius of hemispherical portion = r = 6 cm

Height of cylindrical portion (H) = 14 cm

Volume of liquid = Volume of cylindrical portion (upto height 14 cm) + Volume of hemispherical portion

$= πr^2H + \dfrac{2}{3}πr^3 \\[1em] = πr\Big(rH + \dfrac{2}{3}r^2\Big) \\[1em] = \dfrac{22}{7} \times 6 \times \Big(6 \times 14 + \dfrac{2}{3} \times 6^2\Big) \\[1em] = \dfrac{22}{7} \times 6 \times (84 + 24) \\[1em] = \dfrac{132}{7} \times 108 \\[1em] = \dfrac{14256}{7} \text{ cm}^3$

Since, volume of liquid in both vessels is same.

Let height upto which the liquid remains in vessel b is h cm.

From figure (b),

Volume of liquid = Volume of cylindrical portion (upto h cm)

$\therefore \dfrac{14256}{7} = \dfrac{22}{7} \times 6^2 \times h \\[1em] \Rightarrow h = \dfrac{14256 \times 7}{7 \times 22 \times 6^2} \\[1em] \Rightarrow h = \dfrac{14256}{22 \times 36} \\[1em] \Rightarrow h = \dfrac{14256}{792} = 18 \text{ cm}.$

Hence, height upto which the liquid in figure (b) will stand = 18 cm.