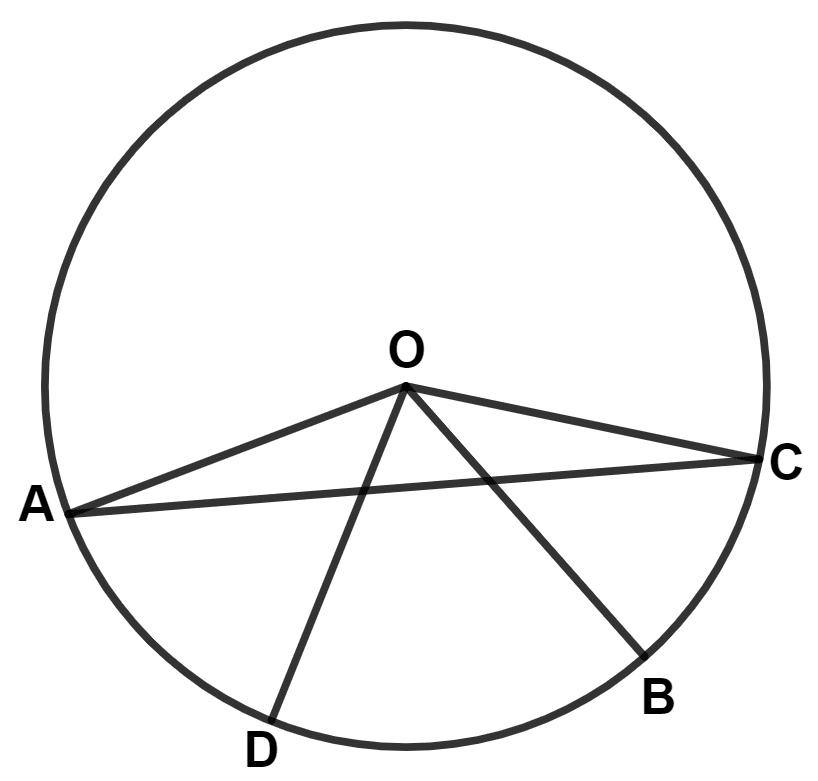
The given figure shows a circle with center O. Points A, D, B and C lie on the circumference of the given circle and angle AOB = 108°. If arc ADB = 2 × arc BC, find :

(i) ∠ACB

(ii) ∠CAB

(iii) ∠ADB

(i) Join BC.

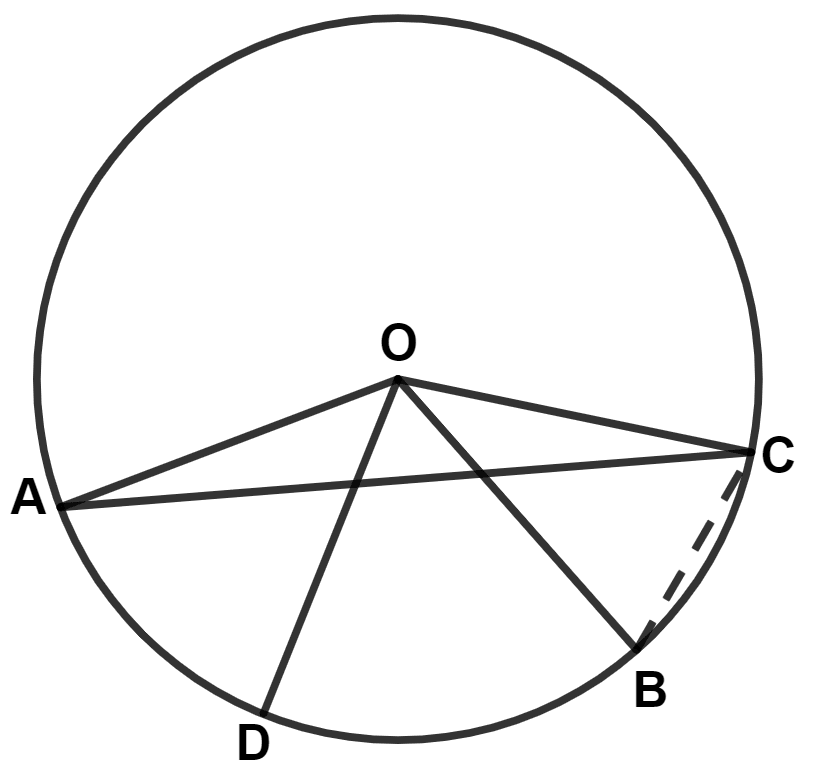
Given,

⇒ arc ADB = 2 × arc BC

⇒ ∠AOB = 2∠BOC

∠BOC = $\dfrac{1}{2}∠AOB = \dfrac{1}{2} \times 108°$ = 54°.

In △ AOC,

⇒ OA = OC (Radius of circle)

⇒ ∠OAC = ∠OCA = y (let) [Angles opposite to equal sides are equal]

By angle sum property of triangle,

⇒ ∠OAC + ∠OCA + ∠AOC = 180°

⇒ y + y + (108° + 54°) = 180° [∵ ∠AOC = ∠AOB + ∠BOC]

⇒ 2y = 180° - 162°

⇒ 2y = 18°

⇒ y = $\dfrac{18°}{2}$ = 9°.

⇒ ∠OCA = 9°

In △ BOC,

⇒ OB = OC (Radius of circle)

⇒ ∠OBC = ∠OCB = x (let) [Angles opposite to equal sides are equal]

By angle sum property of triangle,

⇒ ∠OBC + ∠OCB + ∠BOC = 180°

⇒ x + x + 54° = 180°

⇒ 2x = 180° - 54°

⇒ 2x = 126°

⇒ x = $\dfrac{126°}{2}$ = 63°.

⇒ ∠OCB = 63°

From figure,

⇒ ∠ACB = ∠OCB - ∠OCA = 63° - 9° = 54°.

Hence, ∠ACB = 54°.

(ii) We know that,

Angle which and arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference of the circle.

∴ ∠BOC = 2∠CAB

⇒ ∠CAB = $\dfrac{1}{2}∠BOC = \dfrac{1}{2} \times 54°$ = 27°.

Hence, ∠CAB = 27°.

(iii) Arc AB subtends ∠AOB at the centre and ∠ACB at the remaining part of the circle.

∴ ∠AOB = 2∠ACB

∠ACB = $\dfrac{1}{2}∠AOB = \dfrac{1}{2} \times 108°$ = 54°.

In cyclic quadrilateral ADBC,

⇒ ∠ADB + ∠ACB = 180° [∵ Sum of opp ∠'s in cyclic quadrilateral = 180°]

⇒ ∠ADB + 54° = 180°

⇒ ∠ADB = 180° - 54° = 126°.

Hence, ∠ADB = 126°.