Mathematics
If the diagonals of a parallelogram are of equal lengths, the parallelogram is a rectangle. Prove it.
Answer
Given:
A parallelogram ABCD with diagonals AC and BD of equal lengths.
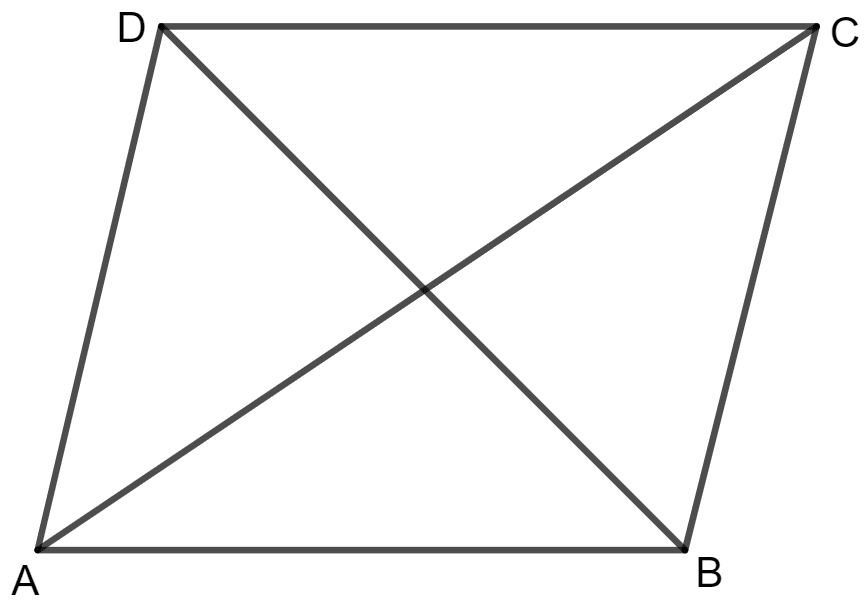
To prove:
The parallelogram ABCD is a rectangle.
Proof:
Consider triangles Δ ABC and Δ ABD:
AB = AB (Common side)
AC = BD (Given)
BC = AD (opposite sides of parallelogram)
By Side Side Side congruency,
Δ ABC ≅ Δ ABD
By using Corresponding Parts of Congruent Triangles,
∠ A = ∠ B
But we know that adjacent angles of parallelogram are supplementary.
∠ A + ∠ B = 180°
∠ A = ∠ B = 90°
Similarly, ∠ C = ∠ D = 90°
Hence, if the diagonals of a parallelogram are of equal lengths, the parallelogram is a rectangle.
Related Questions
ABCD is a parallelogram. What kind of quadrilateral is it if :
(i) AC = BD and AC is perpendicular to BD ?
(ii) AC is perpendicular to BD but is not equal to it ?
(iii) AC = BD but AC is not perpendicular to BD?
Prove that the diagonals of a parallelogram bisect each other.
In parallelogram ABCD, E is the mid-point of AD and F is the mid-point of BC. Prove that BFDE is a parallelogram.
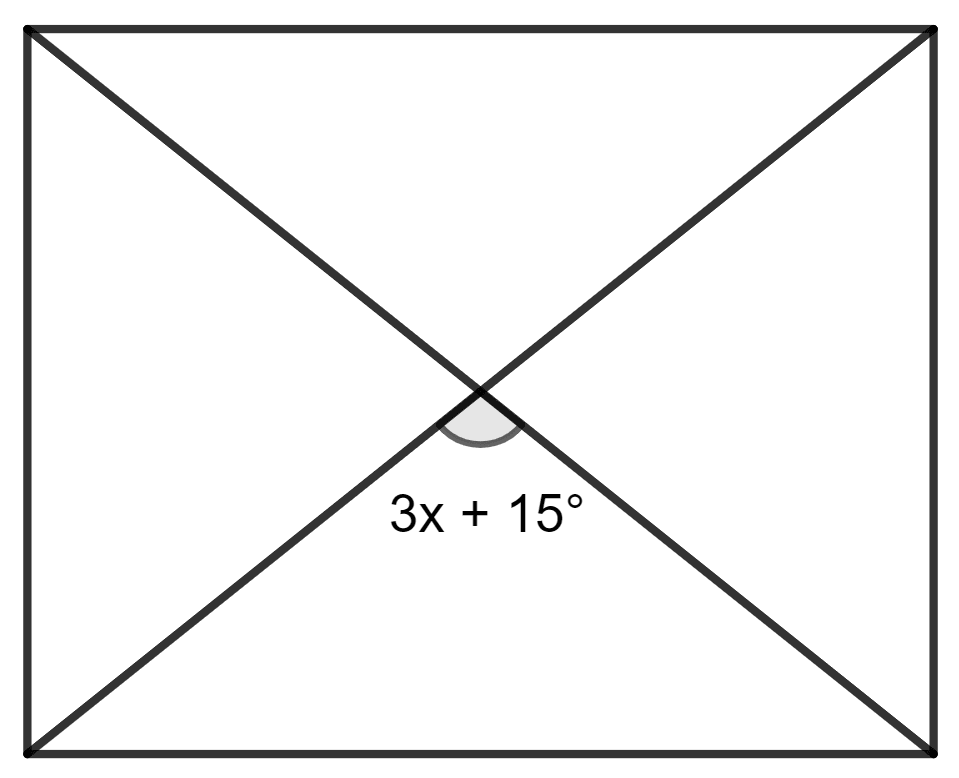
The given figure shows a parallelogram. The value of x for which it will be a rhombus is :
35°
25°
15°
45°