Mathematics
Answer
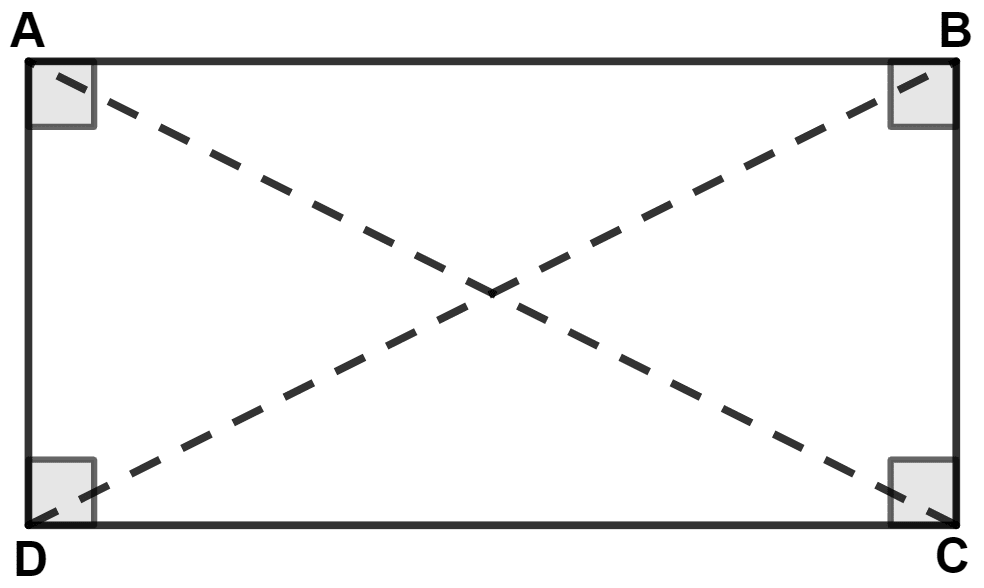
In rectangle the interior angles equal to 90° and opposite sides are equal.
∴ ∠A = ∠B = ∠C = ∠D = 90°, AB = DC and BC = AD.
By formula,
By pythagoras theorem,
⇒ (Hypotenuse)2 = (Perpendicular)2 + (Base)2
In right-angled △ ACD,
⇒ AC2 = AD2 + CD2 ……..(1)
In right-angled △ BCD,
⇒ BD2 = BC2 + CD2
⇒ BD2 = BC2 + AB2 (As CD = AB) ………(2)
Adding equation (1) and (2), we get :
⇒ AC2 + BD2 = AD2 + CD2 + BC2 + AB2.
Hence, proved that AC2 + BD2 = AB2 + BC2 + CD2 + DA2.
Related Questions
M and N are the mid-points of the sides QR and PQ respectively of a △ PQR, right-angled at Q. Prove that :
(i) PM2 + RN2 = 5 MN2
(ii) 4 PM2 = 4 PQ2 + QR2
(iii) 4 RN2 = PQ2 + 4 QR2
(iv) 4 (PM2 + RN2) = 5 PR2
In triangle ABC, ∠B = 90° and D is the mid-point of BC. Prove that : AC2 = AD2 + 3CD2.
In a quadrilateral ABCD, ∠B = 90° and ∠D = 90°. Prove that :
2AC2 - AB2 = BC2 + CD2 + DA2.
O is any point inside a rectangle ABCD. Prove that :
OB2 + OD2 = OC2 + OA2.