In △ ABC, E is mid-point of the median AD and BE produced meets side AC at point Q. Show that BE : EQ = 3 : 1.

Draw DY || BQ.

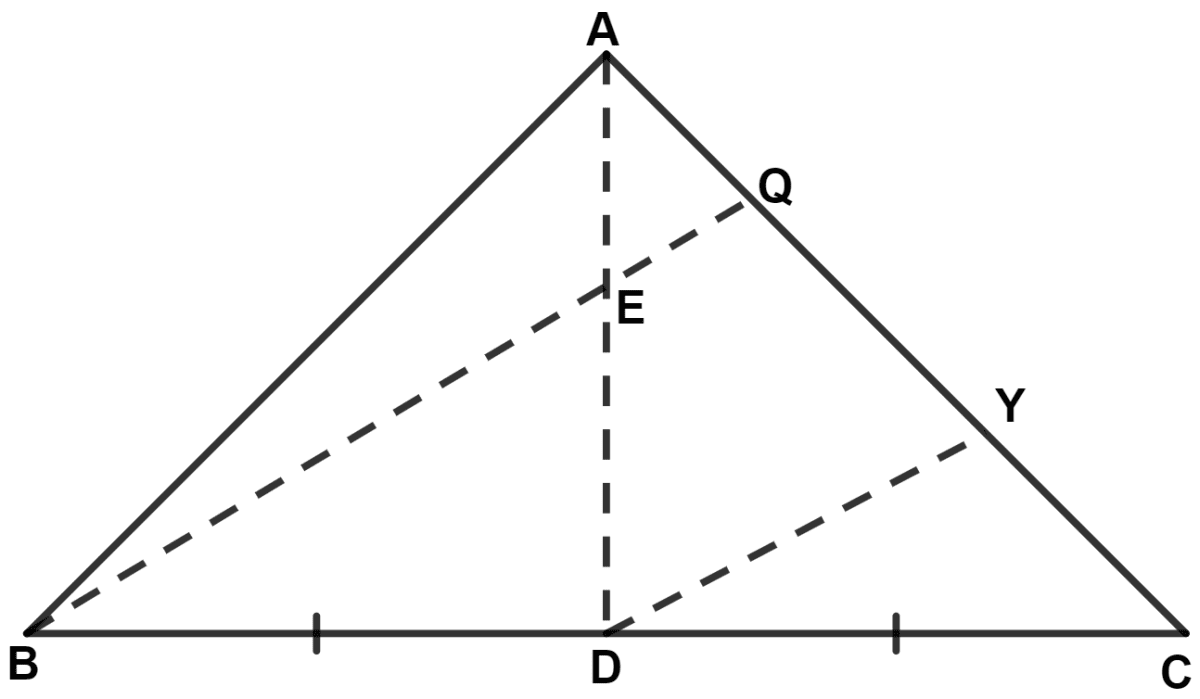
In △ BCQ and △ DCY,

⇒ ∠BCQ = ∠DCY (Common)

⇒ ∠BQC = ∠DYC (Corresponding angles are equal)

∴ △ BCQ ~ △ DCY (By A.A. axiom)

We know that,

Corresponding sides of similar triangle are proportional.

$\Rightarrow \dfrac{BQ}{DY} = \dfrac{BC}{DC} = \dfrac{CQ}{CY}$ ……….(1)

Since, D is the mid-point of BC.

∴ BC = 2CD

Considering L.H.S. of the equation (1), we get :

$\Rightarrow \dfrac{BQ}{DY} = \dfrac{2CD}{DC} \\[1em] \Rightarrow \dfrac{BQ}{DY} = 2 \text{ ……..(1)}$

In △ AEQ and △ ADY,

⇒ ∠EAQ = ∠DAY (Common)

⇒ ∠AEQ = ∠ADY (Corresponding angles are equal)

∴ △ AEQ ~ △ ADY (By A.A. axiom)

We know that,

Corresponding sides of similar triangle are proportional.

$\Rightarrow \dfrac{EQ}{DY} = \dfrac{AE}{AD} = \dfrac{1}{2}$ (Since, E is the mid-point of AD)

$\Rightarrow \dfrac{EQ}{DY} = \dfrac{1}{2}$ …………(2)

Dividing equation (1) by (2), we get :

$\Rightarrow \dfrac{\dfrac{BQ}{DY}}{\dfrac{EQ}{DY}} = \dfrac{2}{\dfrac{1}{2}} \\[1em] \Rightarrow \dfrac{BQ \times DY}{EQ \times DY} = 4 \\[1em] \Rightarrow \dfrac{BQ}{EQ} = 4 \\[1em] \Rightarrow \dfrac{BE + EQ}{EQ} = 4 \\[1em] \Rightarrow BE + EQ = 4EQ \\[1em] \Rightarrow BE = 4EQ - EQ \\[1em] \Rightarrow BE = 3EQ \\[1em] \Rightarrow \dfrac{BE}{EQ} = \dfrac{3}{1}.$

Hence, proved that BE : EQ = 3 : 1.