Mathematics
In each of the following cases ABCD is a square and PQRS is a rectangle. Find, in each case, the area of the shaded portion. (All measurements are in metre).
(i)
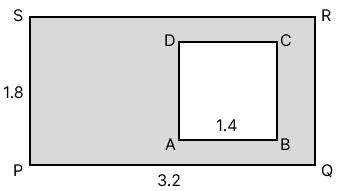
(ii)

Area Trapezium Polygon
11 Likes
Answer
(i) The area of the shaded portion = Area of the rectangle - Area of the square.
It is given that the length and breadth of the rectangle area 3.2 m and 1.8 m.
As we know, the area of the rectangle = length x breadth
= 3.2 x 1.8 m2
= 5.76 m2
The side of the square is 1.4 m.
And, the area of the square = side2
= 1.42 m2
= 1.96 m2
Thus, the area of the shaded portion = 5.76 - 1.96 m2
= 3.8 m2
Hence, the area of the shaded portion is 3.8 m2.
(ii) The area of the shaded portion = Area of the square - Area of the rectangle.
It is given that the side of the square is 6 m.
And, the area of the square = side2
= 62 m2
= 36 m2
The length and breadth of the rectangle are 4.8 m and 3.6 m, respectively.
As we know, the area of the rectangle = length x breadth
= 4.8 x 3.6 m2
= 17.28 m2
Area of the shaded portion = 36 - 17.28 m2
= 18.72 m2
Hence, the area of the shaded portion is 18.72 m2.
Answered By
7 Likes
Related Questions
The perimeter of a square is numerically equal to its area. Find its area.
Each side of a rectangle is doubled. Find the ratio between :
(i) perimeters of the original rectangle and the resulting rectangle
(ii) areas of the original rectangle and the resulting rectangle
A path of uniform width, 3 m, runs around the outside of a square field of side 21 m. Find the area of the path.
A path of uniform width, 2.5 m, runs around the inside of a rectangular field 30 m by 27 m. Find the area of the path.