Mathematics
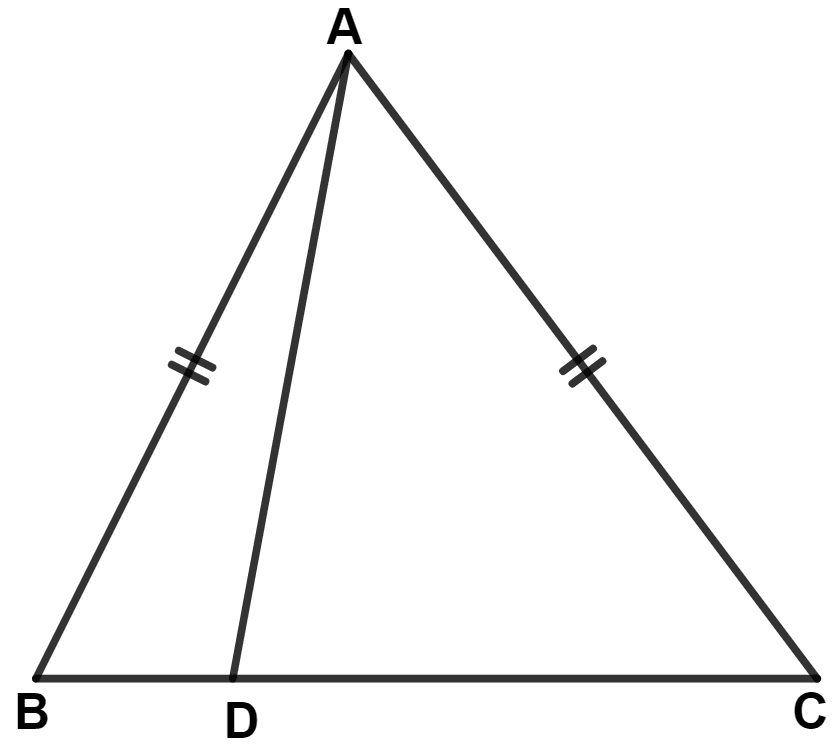
In the figure, AB = AC and D is any point on BC, show that AB > AD.
Triangles
10 Likes
Answer
In △ ABD and △ ACD,
⇒ AB = AC (Given)
⇒ ∠ABC = ∠ACB = θ (let) [Angles opposite to equal sides are equal]
⇒ AD = AD (Common side)
∴ △ ABD ≅ △ ACD (By S.A.S. axiom)
We know that,
Corresponding sides of congruent triangle are equal.
∴ ∠ADB = ∠ADC = x (let)
From figure,
⇒ ∠ADB + ∠ADC = 180°
⇒ x + x = 180°
⇒ 2x = 180°
⇒ x = = 90°.
∴ ∠ADB = ∠ADC = 90°.
We know that,
The base angles of isosceles triangle are acute angles.
∴ θ < 90°
In △ ABD,
⇒ ∠ADB > ∠ABD
⇒ AB > AD. [If two angles of a triangle are unequal, the greater angle has the greater side opposite to it.]
Hence, proved that AB > AD.
Answered By
6 Likes
Related Questions
Prove that the straight line joining the vertex of an isosceles triangle to any point in the base is smaller than either of the equal sides of the triangle.
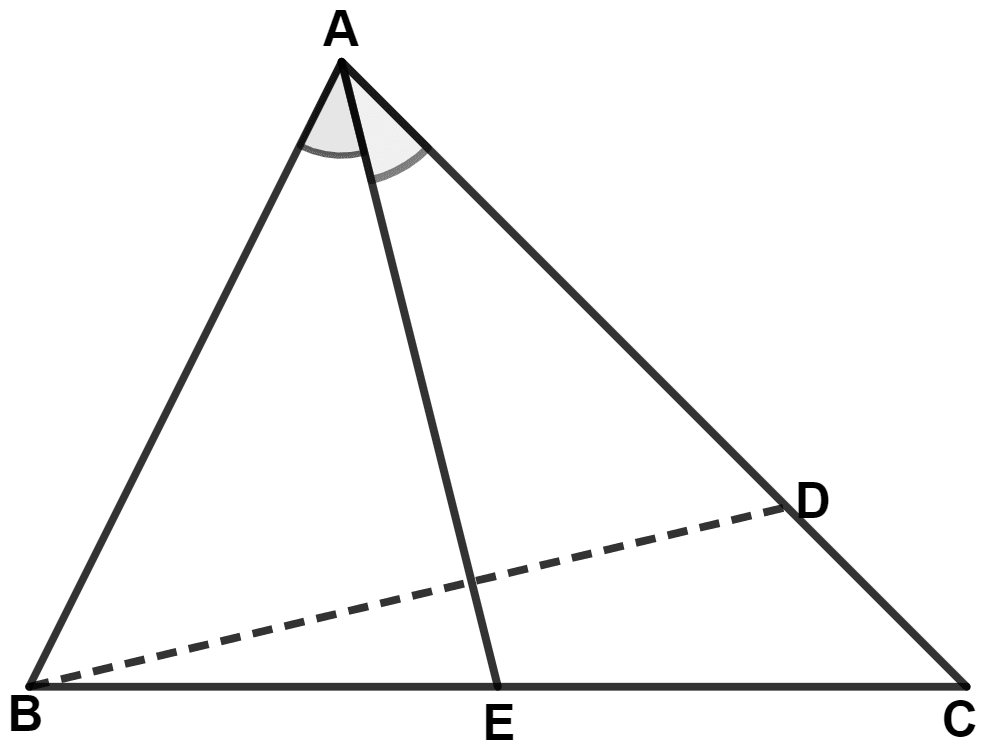
In the following diagram; AD = AB and AE bisects angle A. Prove that :
(i) BE = DE
(ii) ∠ABD > ∠C
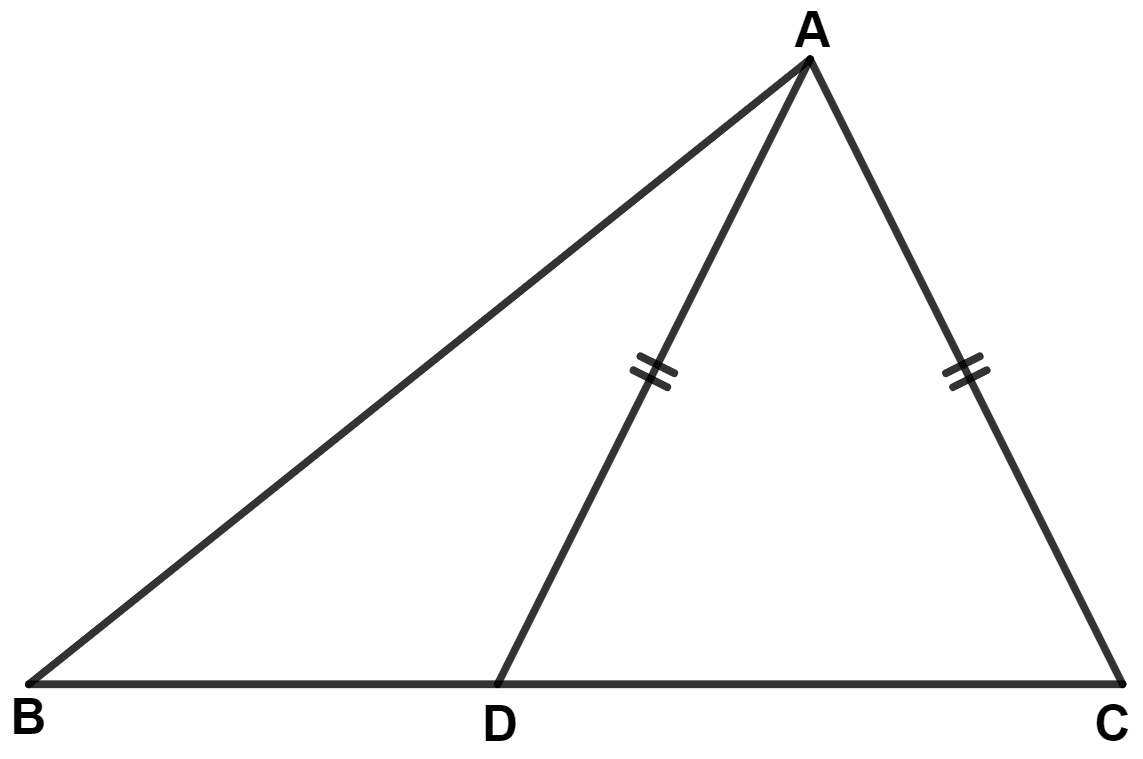
In the given figure, AD = AC and B is a point on CD produced, show that AB > AD.
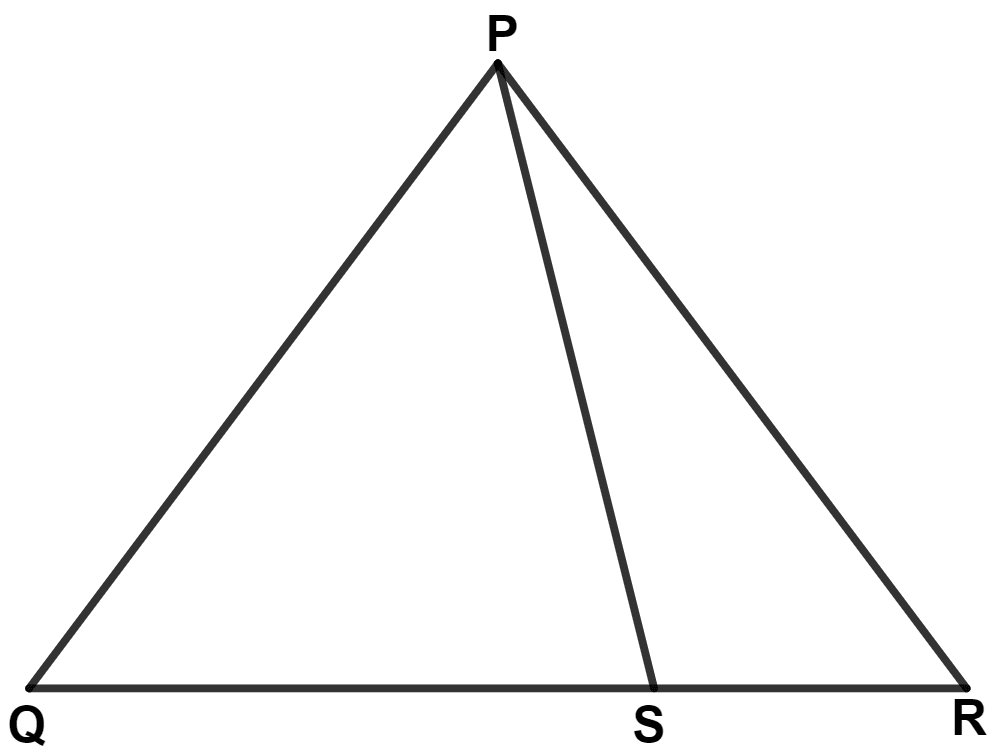
S is any point on side QR of triangle PQR. Prove that :
PQ + QR + RP > 2PS