Mathematics
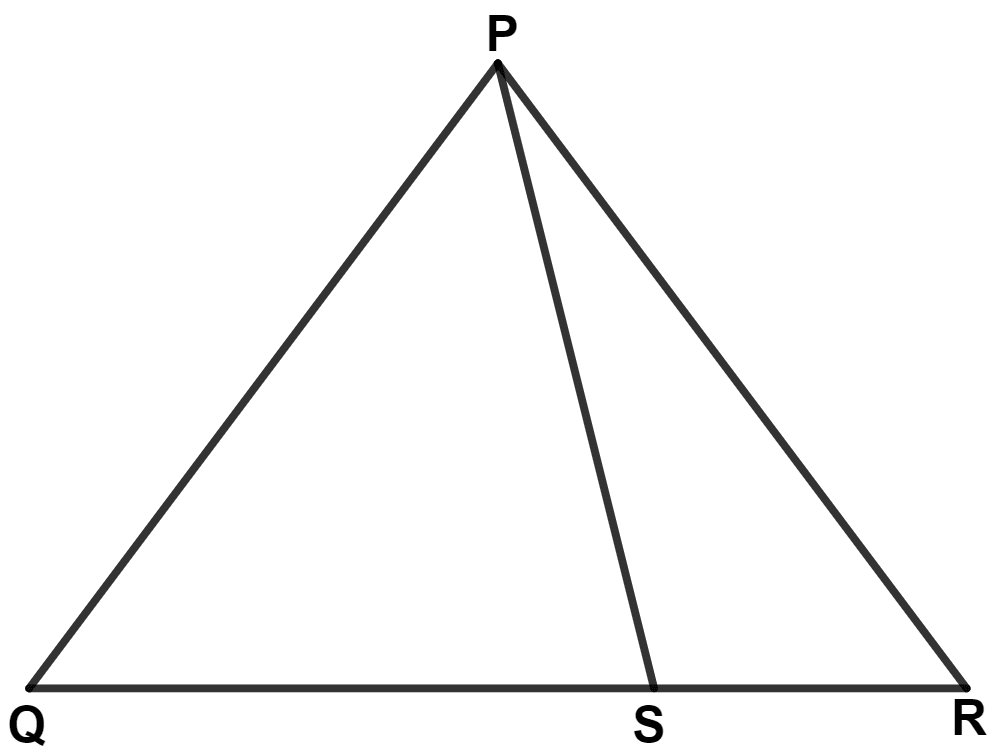
S is any point on side QR of triangle PQR. Prove that :
PQ + QR + RP > 2PS
Triangles
7 Likes
Answer
In △ PQS,
⇒ PQ + QS > PS ……..(1) [Sum of any two sides of a triangle is greater than the third side]
In △ PRS,
⇒ RP + RS > PS ……..(2) [Sum of any two sides of a triangle is greater than the third side]
Adding equations (1) and (2), we get :
⇒ PQ + QS + RP + RS > PS + PS
⇒ PQ + (QS + RS) + RP > 2PS
⇒ PQ + QR + RP > 2PS.
Hence, proved that PQ + QR + RP > 2PS.
Answered By
3 Likes
Related Questions
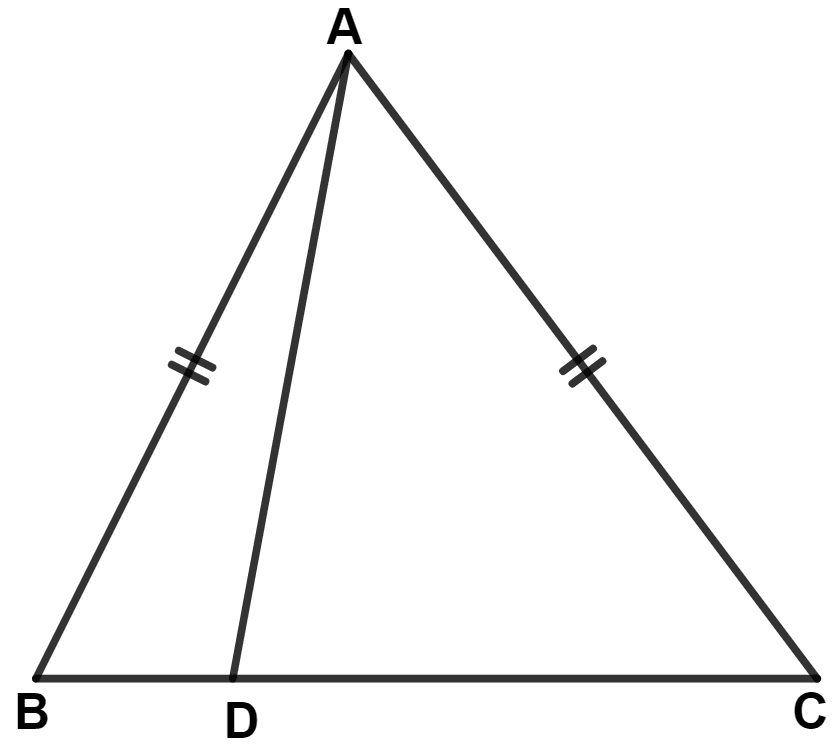
In the figure, AB = AC and D is any point on BC, show that AB > AD.
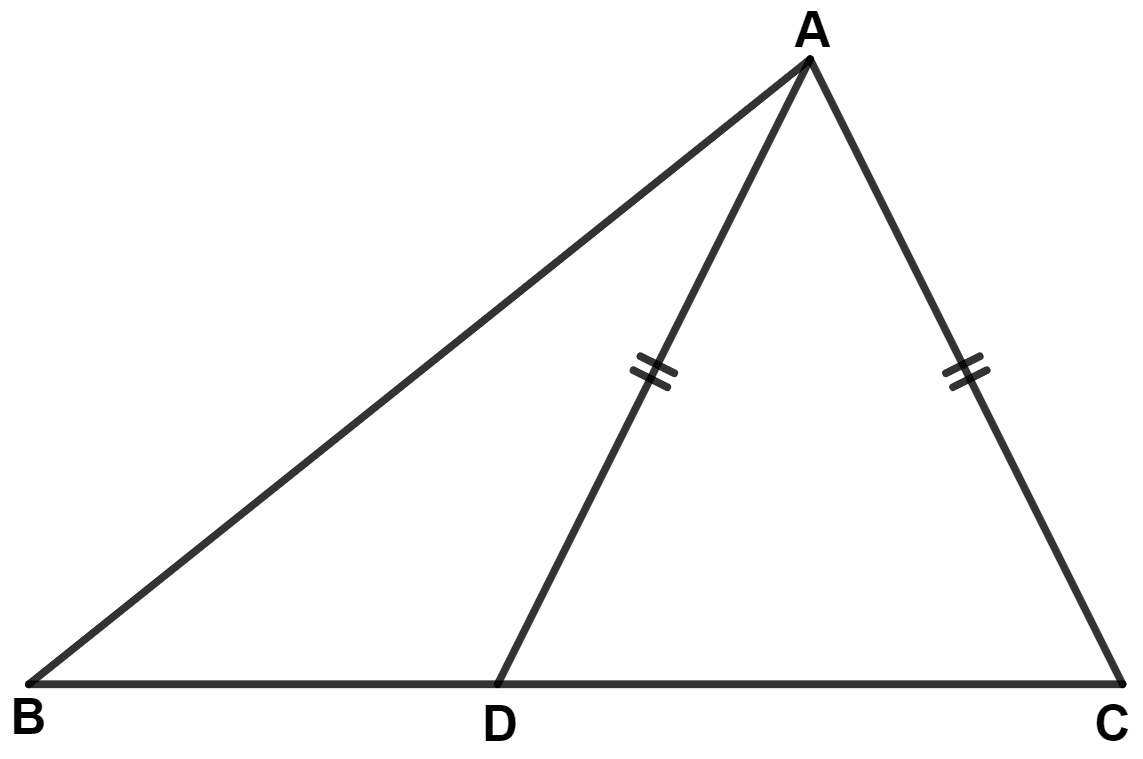
In the given figure, AD = AC and B is a point on CD produced, show that AB > AD.
The sides AB and AC of a triangle ABC are produced; and the bisectors of the external angles at B and C meet at P. Prove that if AB > AC, then PC > PB.
In the following figure; AB is the largest side and BC is the smallest side of triangle ABC.
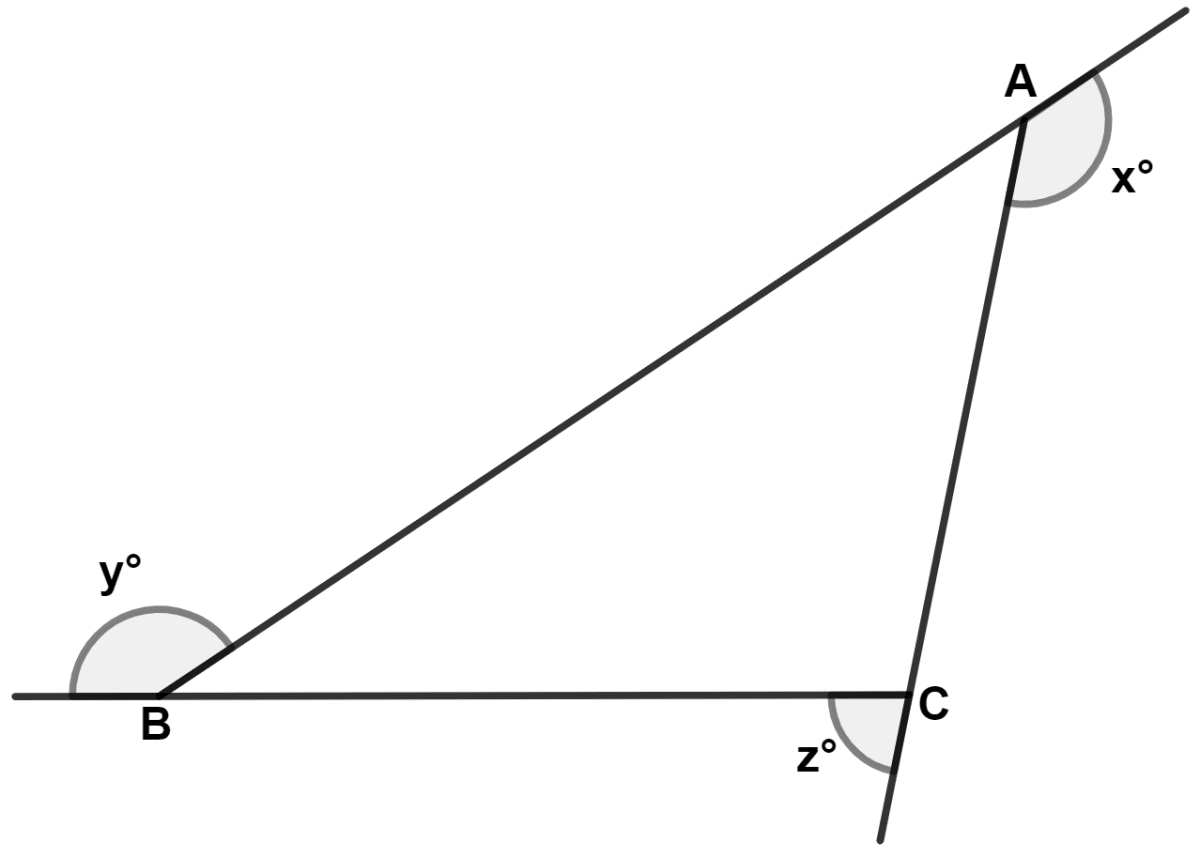
Write the angles x°, y° and z° in ascending order of their values.