Mathematics
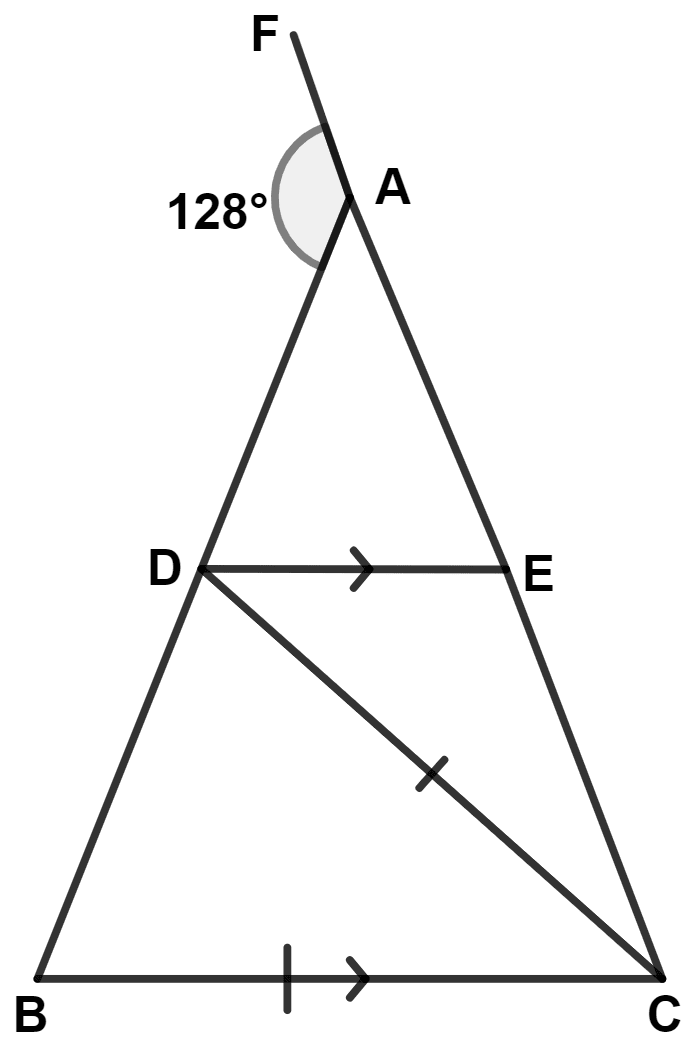
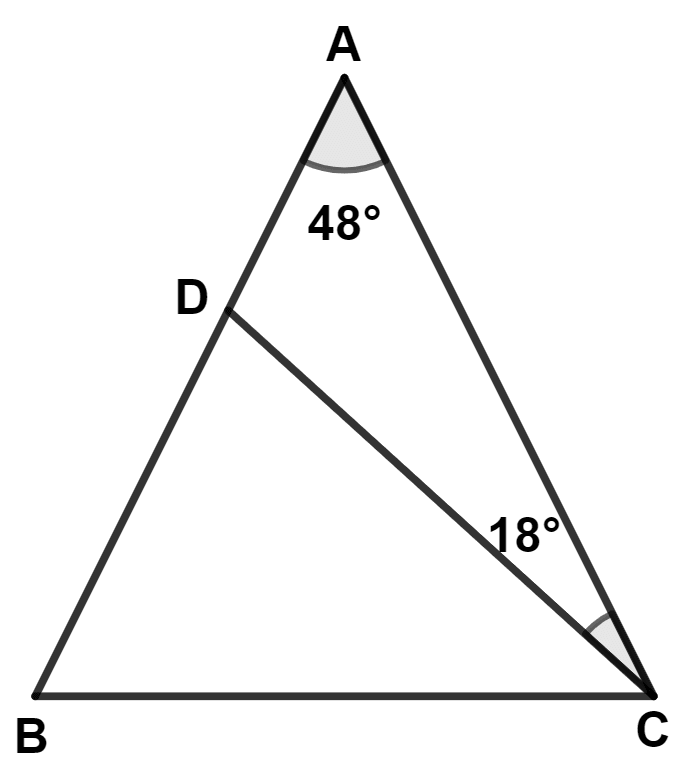
In the figure alongside,
AB = AC
∠A = 48° and
∠ACD = 18°.
Show that : BC = CD.
Triangles
72 Likes
Answer
In △ ABC,
⇒ AB = AC (Given)
⇒ ∠C = ∠B = x (let) (Angles opposite to equal sides are equal)
By angle sum property of triangle,
⇒ ∠A + ∠B + ∠C = 180°
⇒ 48° + x + x = 180°
⇒ 48° + 2x = 180°
⇒ 2x = 180° - 48°
⇒ 2x = 132°
⇒ x = = 66°.
∴ ∠B = ∠C = 66°.
From figure,
⇒ ∠DCB = ∠C - ∠ACD = 66° - 18° = 48°.
In △ BDC,
By angle sum property of triangle,
⇒ ∠BDC + ∠DCB + ∠CBD = 180°
⇒ ∠BDC + 48° + 66° = 180°
⇒ ∠BDC + 114° = 180°
⇒ ∠BDC = 180° - 114° = 66°.
Since, ∠BDC = ∠CBD
∴ BC = CD (Sides opposite to equal angles are equal).
Hence, proved that BC = CD.
Answered By
46 Likes
Related Questions
In the given figure; BE = DC, then :
AD = DC
AE = BE
AD = AE
∠ABE = ∠DAC
In △ ABC and △ PQR, AB = AC, ∠C = ∠P and ∠B = ∠Q; then triangles are :
isosceles but not congruent
isosceles and congruent
congruent but not isosceles
neither isosceles nor congruent.
Calculate :
(i) ∠ADC
(ii) ∠ABC
(iii) ∠BAC
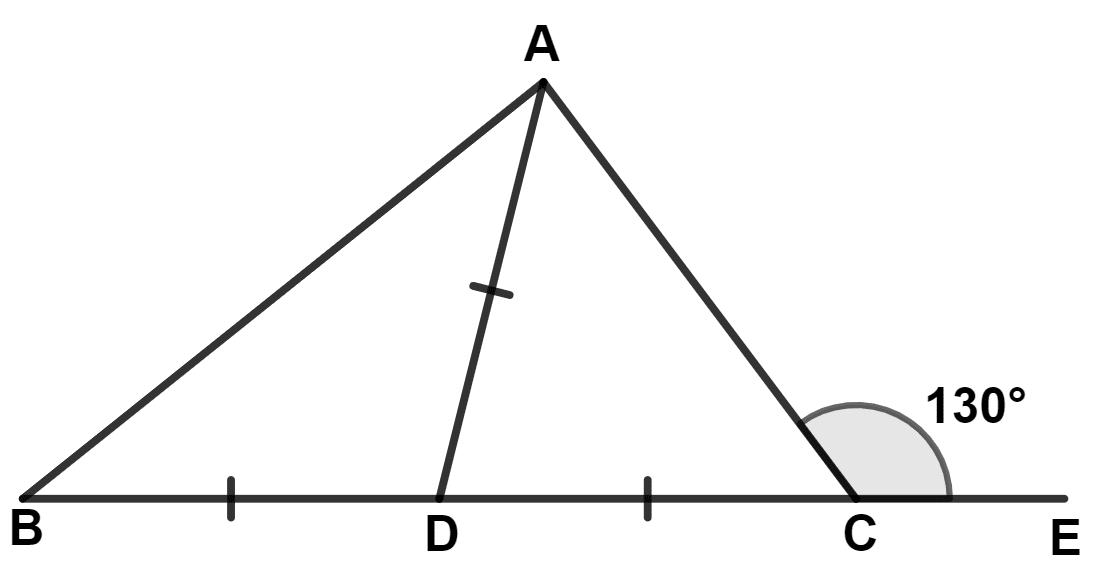
In the following figure, AB = AC; BC = CD and DE is parallel to BC. Calculate :
(i) ∠CDE
(ii) ∠DCE