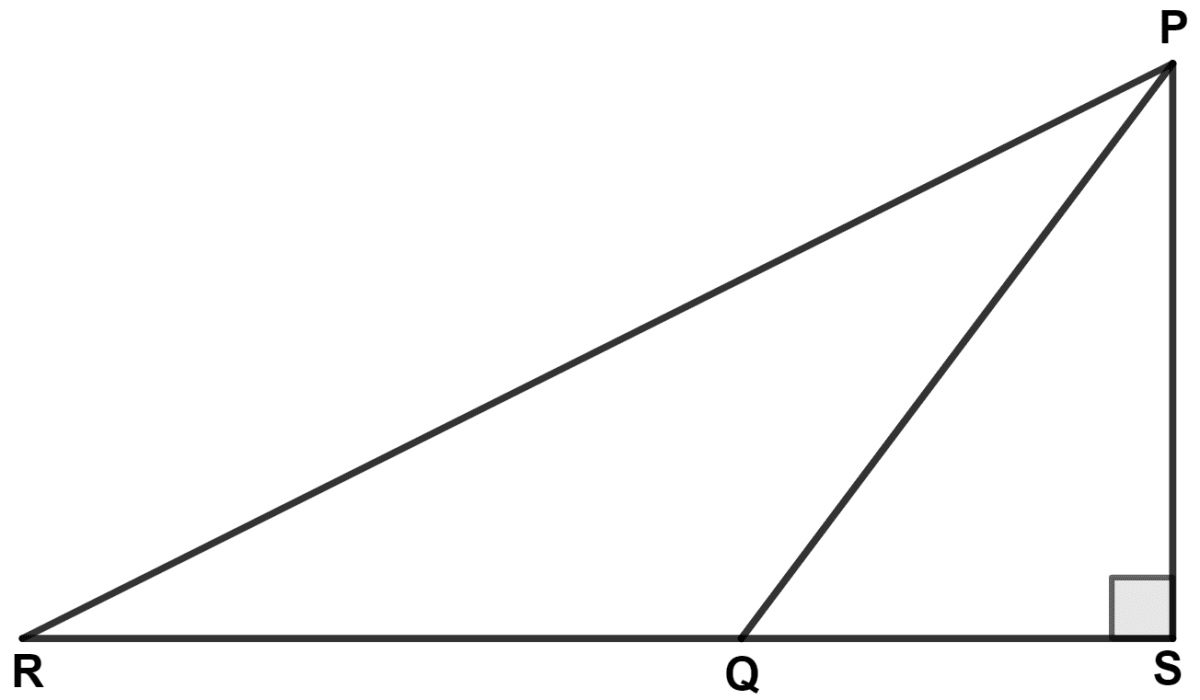
In the figure : ∠PSQ = 90°, PQ = 10 cm, QS = 6 cm and RQ = 9 cm. Calculate the length of PR.

In right angled triangle PQS,

By pythagoras theorem,

⇒ (Hypotenuse)² = (Perpendicular)² + (Base)²

⇒ PQ² = PS² + QS²

⇒ 10² = PS² + 6²

⇒ PS² = 10² - 6²

⇒ PS² = 100 - 36

⇒ PS² = 64

⇒ PS = $\sqrt{64}$ = 8 cm.

From figure,

RS = RQ + QS = 9 + 6 = 15 cm.

In right angled triangle PRS,

By pythagoras theorem,

⇒ (Hypotenuse)² = (Perpendicular)² + (Base)²

⇒ PR² = PS² + RS²

⇒ PR² = 8² + 15²

⇒ PR² = 64 + 225

⇒ PR² = 289

⇒ PR = $\sqrt{289}$ = 17 cm.

Hence, PR = 17 cm.