Mathematics
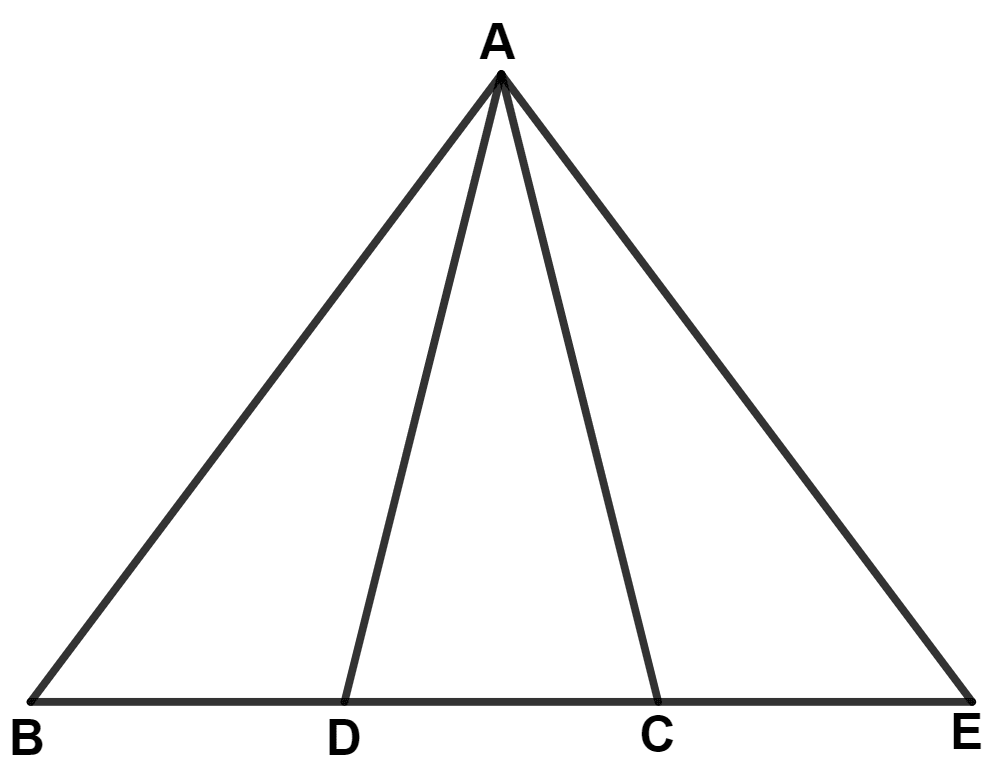
In the following figure, ∠BAD = ∠EAC, BD = EC and ∠B = ∠E, then :
△ ABD ≇ △ AEC
△ ABC ≅ △ AED
△ ABC ≇ △ AED
△ ABD ≅ △ ADE
Answer
Given,
BD = EC = x (let)
∠B = ∠E
We know that,
Sides opposite to equal angles are equal.
∴ AE = AB
From figure,
BC = BD + DC = x + DC …….(1)
DE = DC + CE = DC + x …….(2)
From equations (1) and (2), we get :
BC = DE
In △ ABC and △ AED,
⇒ BC = DE (Proved above)
⇒ AB = AE (Proved above)
⇒ ∠B = ∠E (Given)
∴ △ ABC ≅ △ AED (By S.A.S. axiom)
Hence, Option 2 is the correct option.
Related Questions
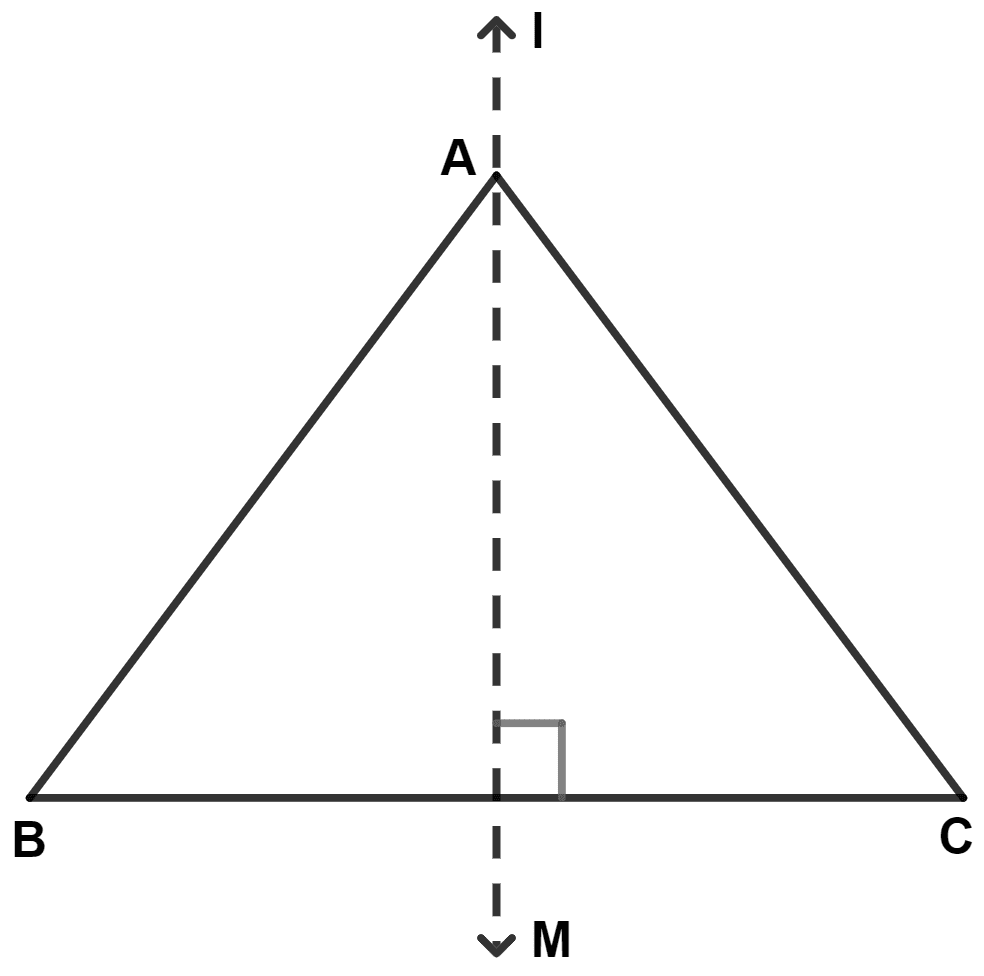
In the given figure, AM is the perpendicular bisector of BC. Then :
AB = AM
AC = BM
AB ≠ AC
AM bisects ∠BAC
Which of the following is true for the given figure:
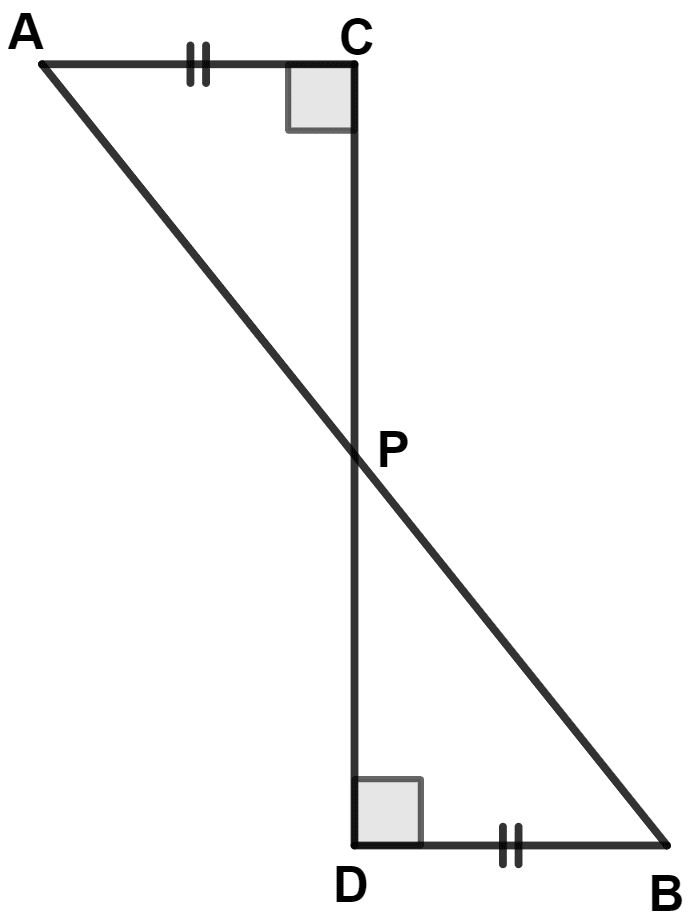
ΔAPC ≅ ΔBPD
CP = DP
AB and CD bisect each other
all of the above are true.
Which of the following is true for the given figure :
△ ABD ≅ △ ACD
angle BAD ≠ angle CAD
△ ABD ≇ △ ACD
∠EAB = ∠BAD
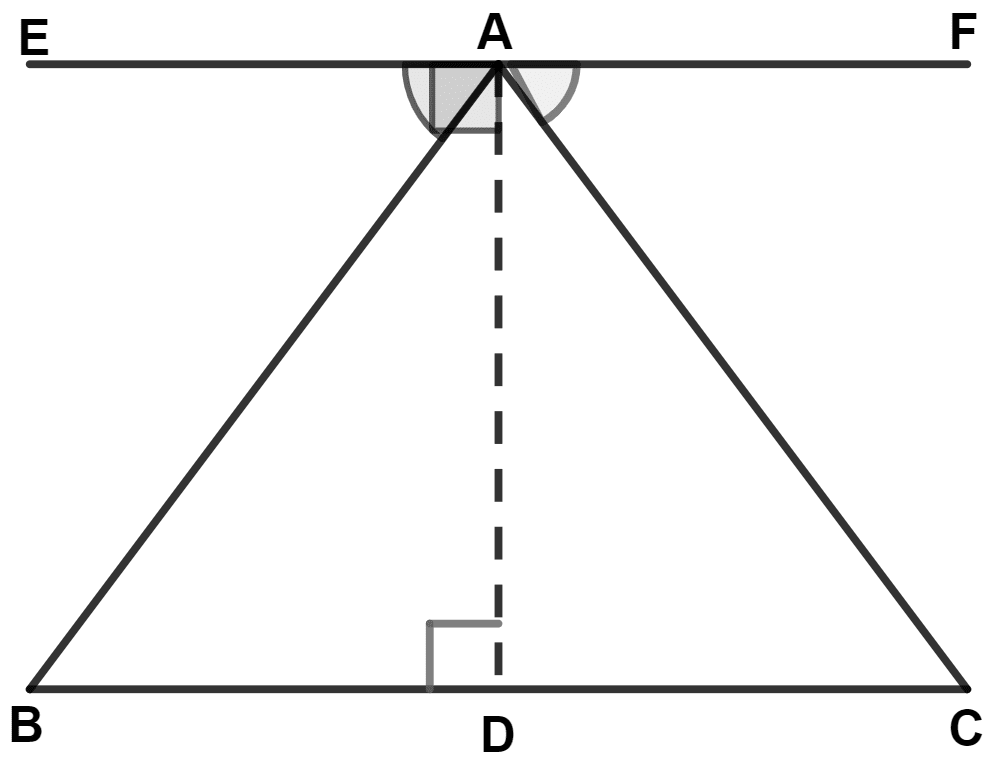
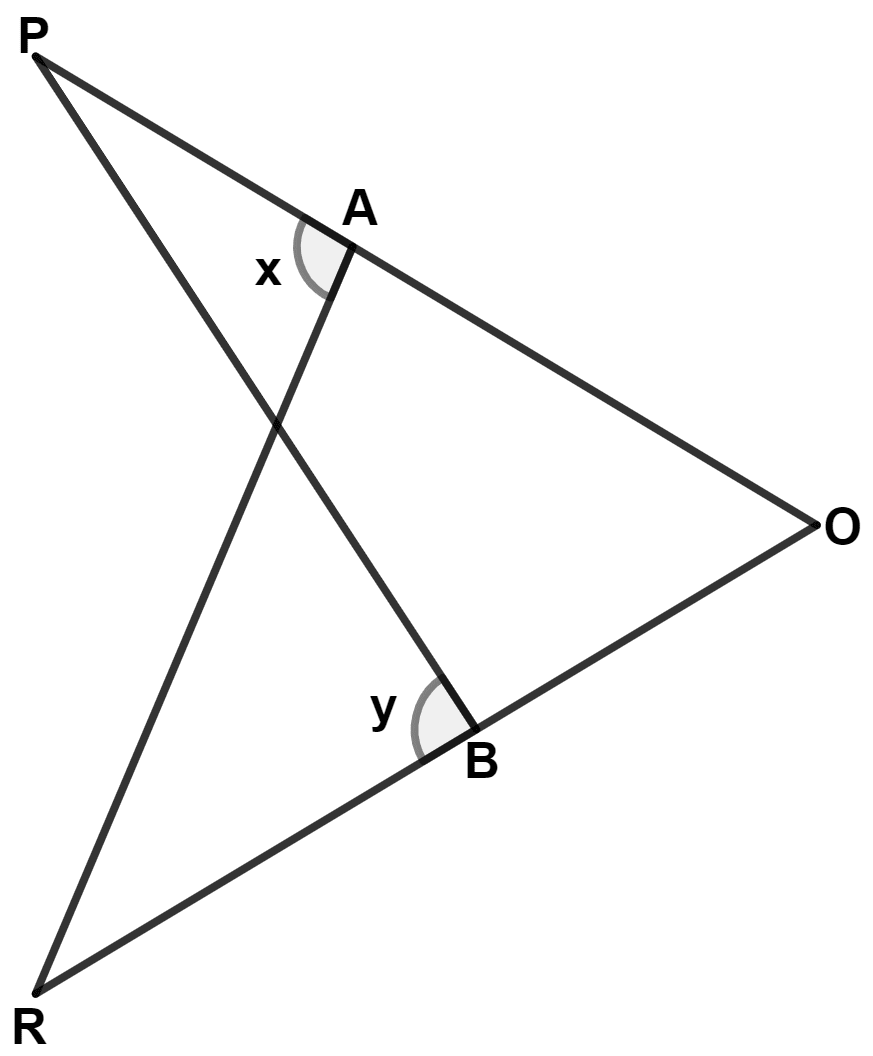
In the given figure, ∠x = ∠y and PO = RO, then :
RB = AO
BO = PA
BP = AR
RB = OB