Mathematics
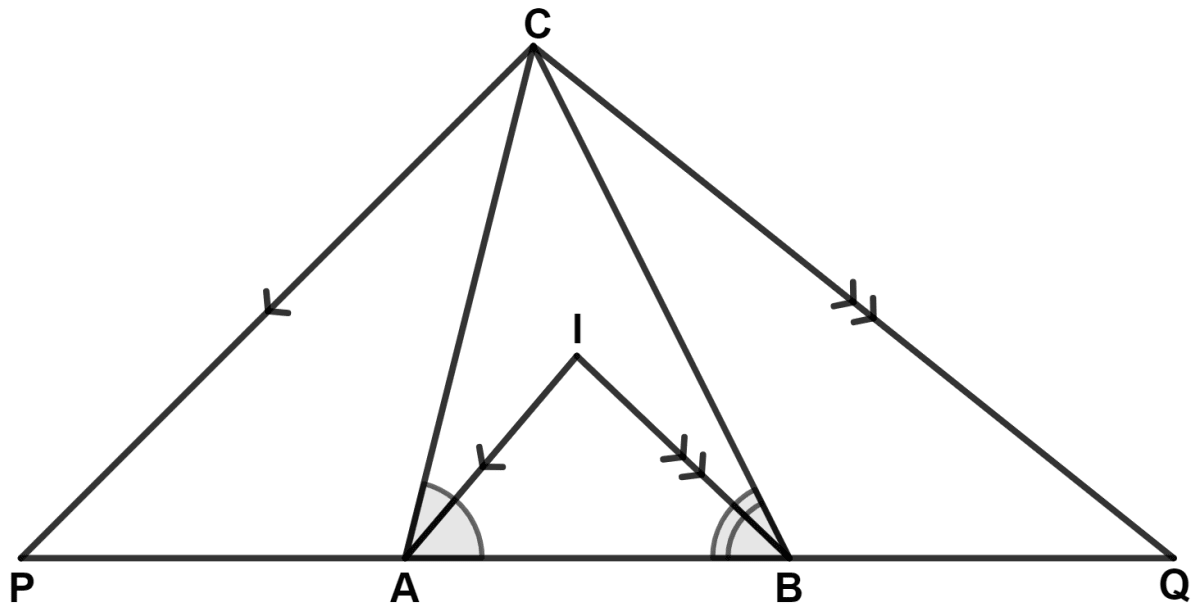
In the following figure; IA and IB are bisectors of angles CAB and CBA respectively. CP is parallel to IA and CQ is parallel to IB.
Prove that :
PQ = The perimeter of Δ ABC.
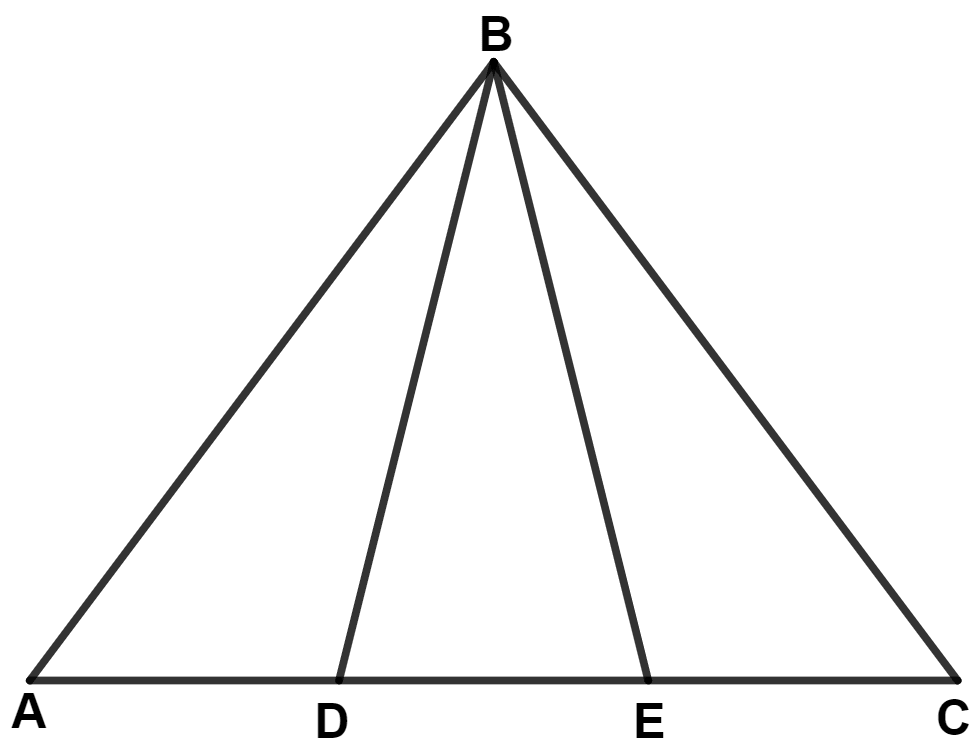
In the given figure; AB = BC and AD = EC. Prove that : BD = BE.
Answer
From figure,
IA || CP and CA is a transversal.
⇒ ∠CAI = ∠PCA (Alternate angles are equal) ………(1)
Also, IA || CP and AP is a transversal
⇒ ∠IAB = ∠APC (Corresponding angles are equal) ……(2)
Since, IA is the bisector of ∠CAB.
∴ ∠CAI = ∠IAB ………(3)
Substituting values from equation (1) and (2) in equation (3), we get :
⇒ ∠PCA = ∠APC
⇒ AC = AP (Sides opposite to equal angles are equal)
From figure,
IB || CQ and CB is a transversal.
⇒ ∠CBI = ∠QCB (Alternate angles are equal) ………(4)
Also, IB || CQ and BQ is a transversal
⇒ ∠IBA = ∠BQC (Corresponding angles are equal) ……(5)
Since, IB is the bisector of ∠CBA.
∴ ∠CBI = ∠IBA ………(6)
Substituting values from equation (4) and (5) in equation (6), we get :
⇒ ∠QCB = ∠BQC
⇒ BQ = BC (Sides opposite to equal angles are equal)
From figure,
PQ = AP + AB + BQ = AC + AB + BC
= Perimeter of △ ABC.
Hence, proved that PQ = Perimeter of △ ABC.
Related Questions
Prove that a triangle ABC is isosceles, if :
(i) altitude AD bisects angle BAC or,
(ii) bisector of angle BAC is perpendicular to base BC.
In the given figure; AB = BC and AD = EC. Prove that : BD = BE.
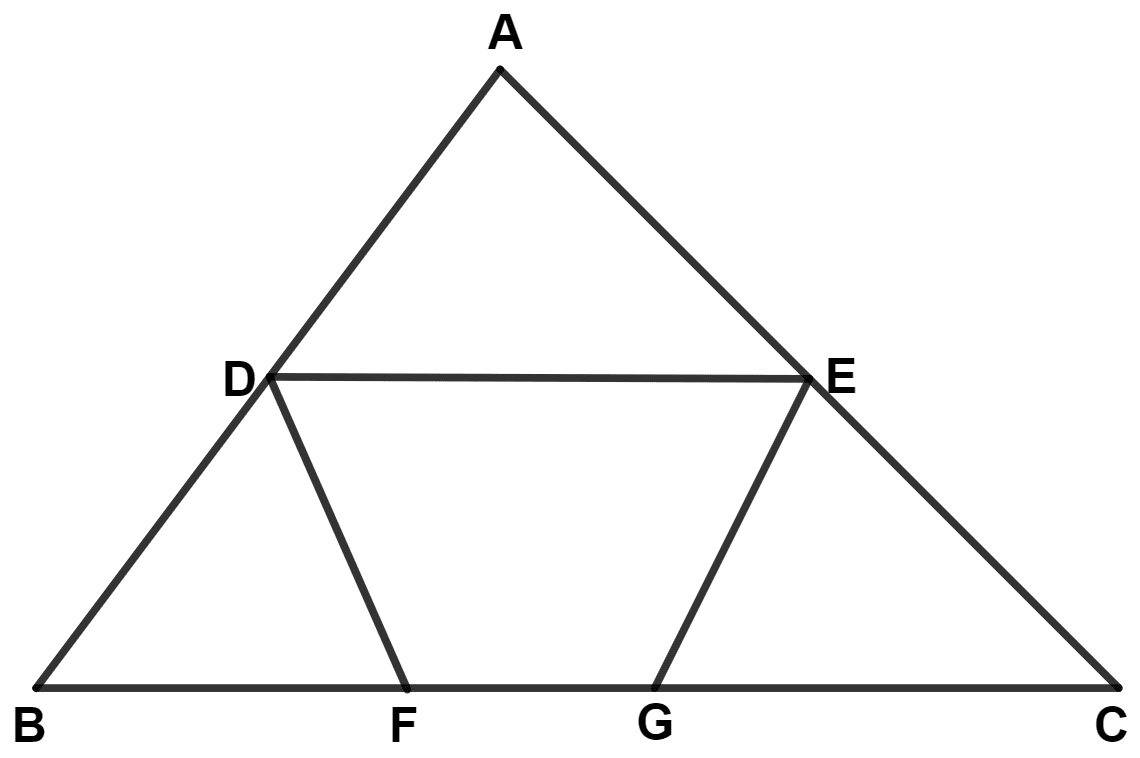
The given figure shows an equilateral triangle ABC with each side 15 cm. Also DE // BC, DF // AC and EG //AB. If DE + DF + EG = 20 cm, find FG.
In triangle ABC, bisector of angle BAC meets opposite side BC at point D. If BD = CD, prove that △ ABC is isosceles.