Mathematics
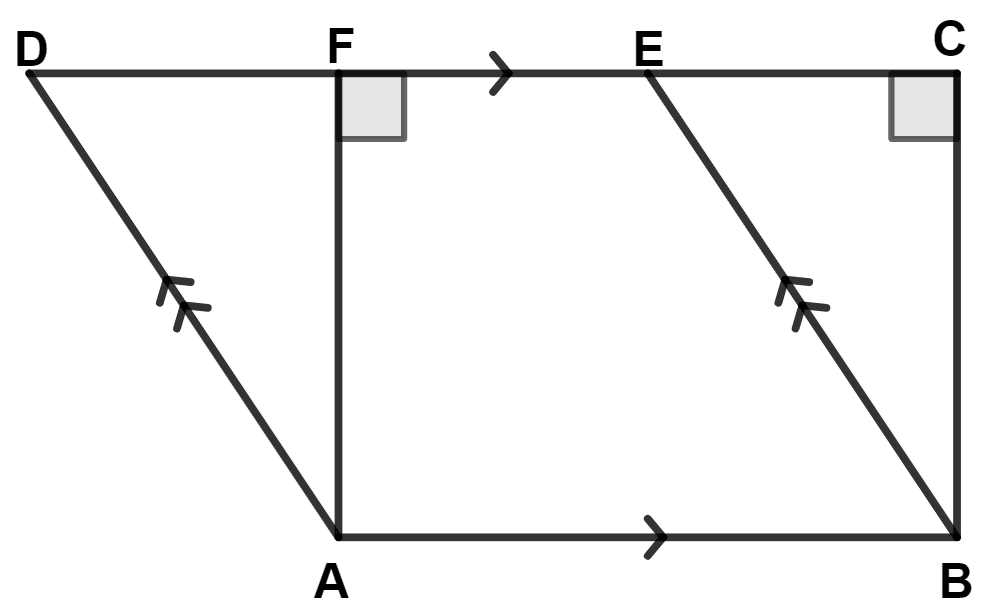
In the given figure, if area of triangle ADE is 60 cm2; state, giving reason, the area of :
(i) parallelogram ABED;
(ii) rectangle ABCF;
(iii) triangle ABE.
Theorems on Area
24 Likes
Answer
(i) We know that,
Area of triangle is half that of a parallelogram, on the same base and between the same parallels.
From figure,
△ ADE and parallelogram ABED lies on same base DE and between same parallel lines AB and DE.
∴ Area of △ ADE = Area of parallelogram ABED
⇒ Area of parallelogram ABED = 2 × Area of △ ADE
⇒ Area of parallelogram ABED = 2 × 60 = 120 cm2.
Hence, area of parallelogram ABED = 120 cm2.
(ii) We know that,
Area of parallelogram is equal to area of a rectangle on the same base and between same parallel lines.
From figure,
Parallelogram ABED and rectangle ABCF lie on lie on same base AB and between same parallel lines AB and CD.
∴ Area of rectangle ABCF = Area of parallelogram ABED = 120 cm2.
Hence, area of rectangle ABCF = 120 cm2.
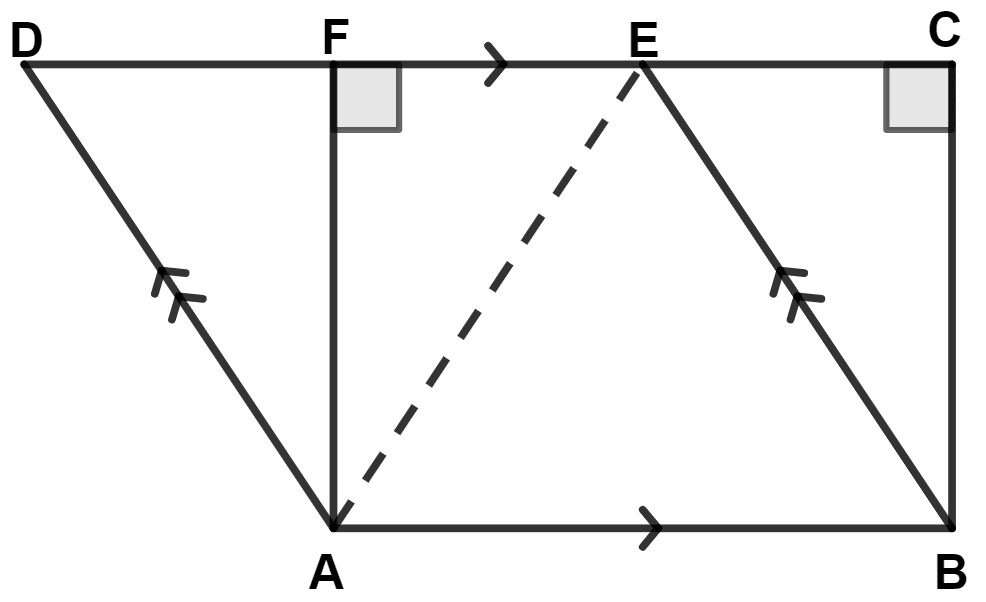
(iii) We know that,
Area of a triangle is half that of a parallelogram on the same base and between the same parallels.
∴ Area of triangle ABE = Area of parallelogram ABED
= = 60 cm2.
Hence, area of triangle ABE = 60 cm2.
Answered By
19 Likes
Related Questions
In the given figure, AF // BE and PQ // RS, FC and ED are perpendiculars to RS. The area of parallelogram ABEF is equal to :
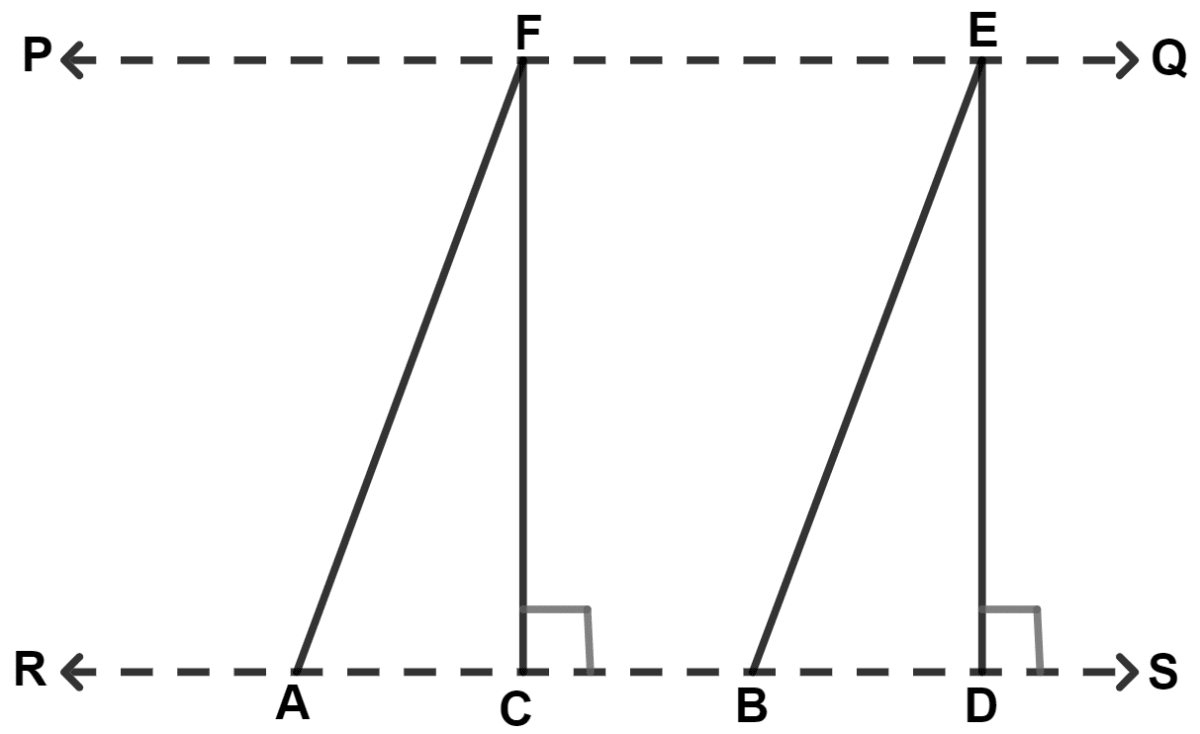
rect. CDEF
quad. CBEF
2 × △ACF
2 × △EBD
In the given figure, D is mid-point of side BC, the area of triangle BEA is equal to area of triangle :
BED
CED
CEA
ACD
The given figure shows a rectangle ABDC and a parallelogram ABEF; drawn on opposite sides of AB. Prove that :
(i) quadrilateral CDEF is a parallelogram
(ii) Area of quad. CDEF = Area of rect. ABDC + Area of // gm ABEF
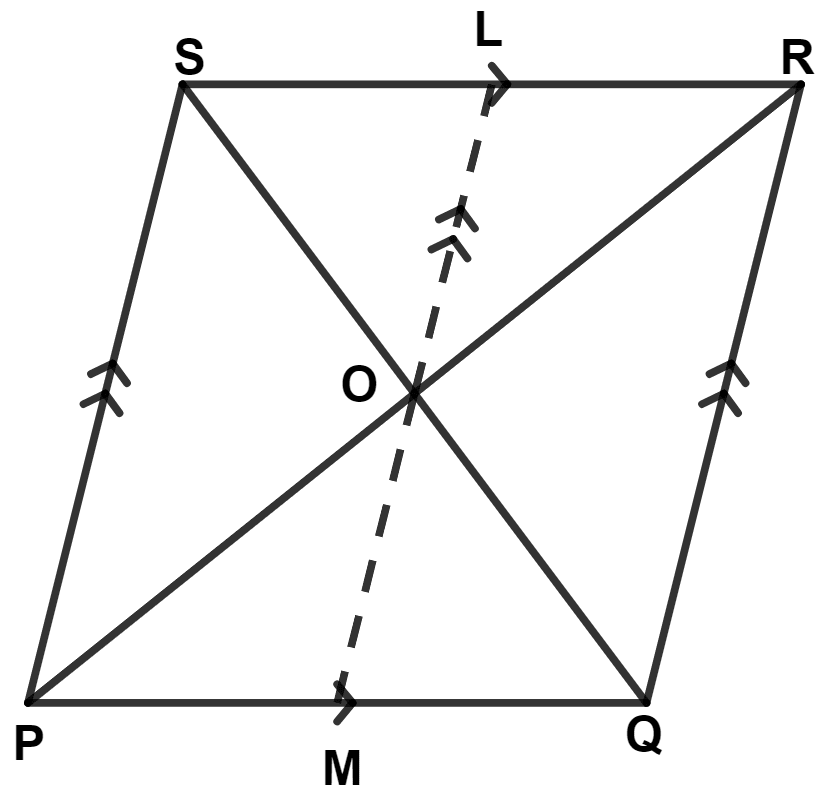
In the given figure, diagonals PR and QS of the parallelogram PQRS intersect at point O and LM is parallel to PS. Show that :
(i) 2 Area (△ POS) = Area (// gm PMLS)
(ii) Area (△ POS) + Area (△ QOR) = Area (//gm PQRS)
(iii) Area (△ POS) + Area (△ QOR) = Area (△ POQ) + Area (△ SOR)