Mathematics
In the given figure, D is mid-point of side BC, the area of triangle BEA is equal to area of triangle :
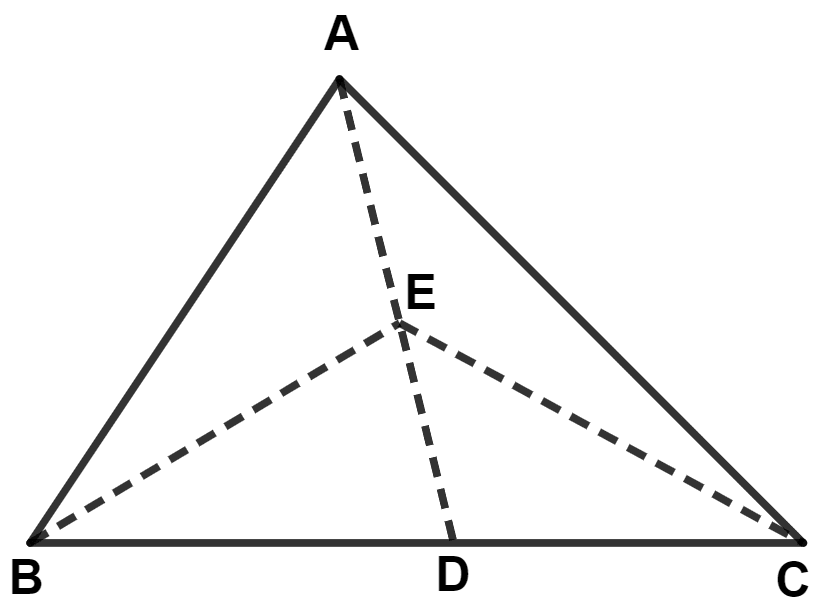
BED
CED
CEA
ACD
Theorems on Area
12 Likes
Answer
In △ ABC,
Since, D is the mid-point of side BC.
∴ AD is the median of BC.
∴ Area of △ ABD = Area of △ ACD (As, median of a triangle divides it into two triangles of equal areas.) ………..(1)
In △ EBC,
Since, D is the mid-point of side BC.
∴ ED is the median of BC.
∴ Area of △ EBD = Area of △ ECD (As, median of a triangle divides it into two triangles of equal areas.) ………(2)
Subtracting equation (2) from (1), we get :
⇒ Area of △ ABD - Area of △ EBD = Area of △ ACD - Area of △ ECD
⇒ Area of △ BEA = Area of △ CEA.
Hence, Option 3 is the correct option.
Answered By
8 Likes
Related Questions
In the given figure, AB is parallel to DC and AB ≠ DC, the area of △ AOD is equal to area of triangle :
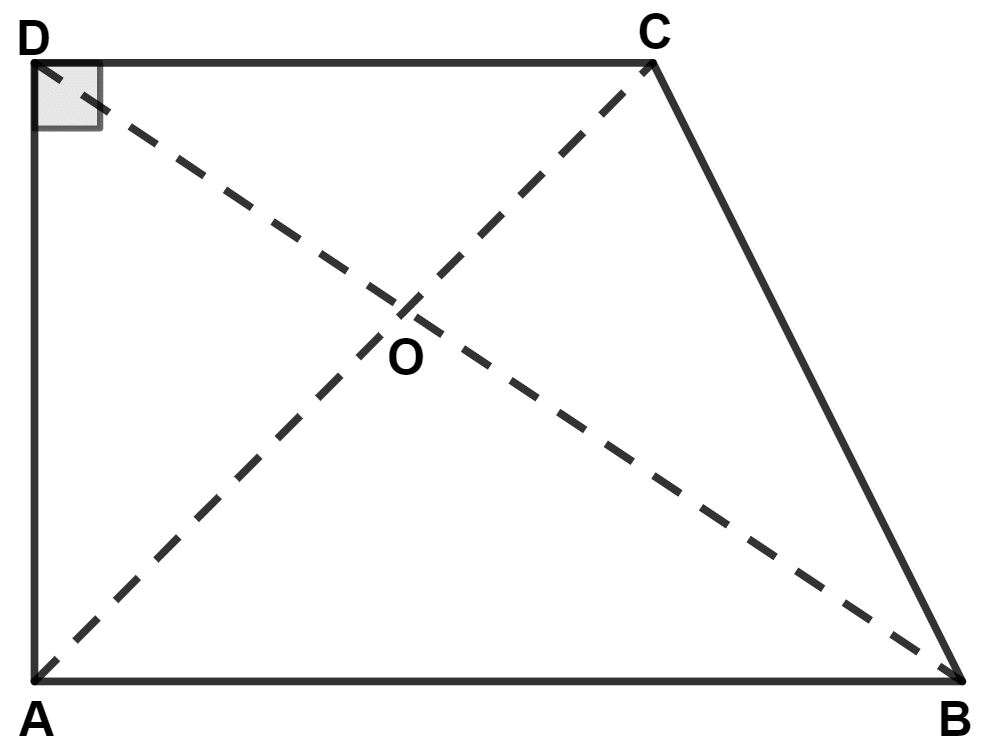
AOB
COD
ACB
BOC
In the given figure, AF // BE and PQ // RS, FC and ED are perpendiculars to RS. The area of parallelogram ABEF is equal to :
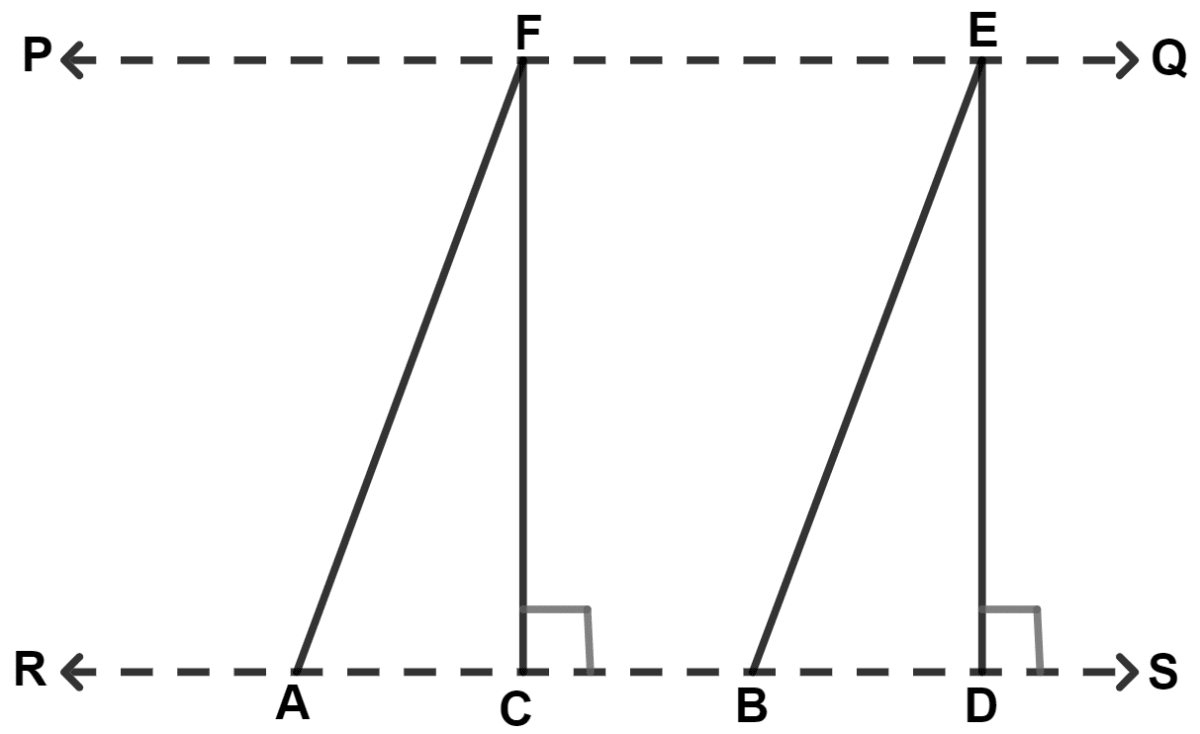
rect. CDEF
quad. CBEF
2 × △ACF
2 × △EBD
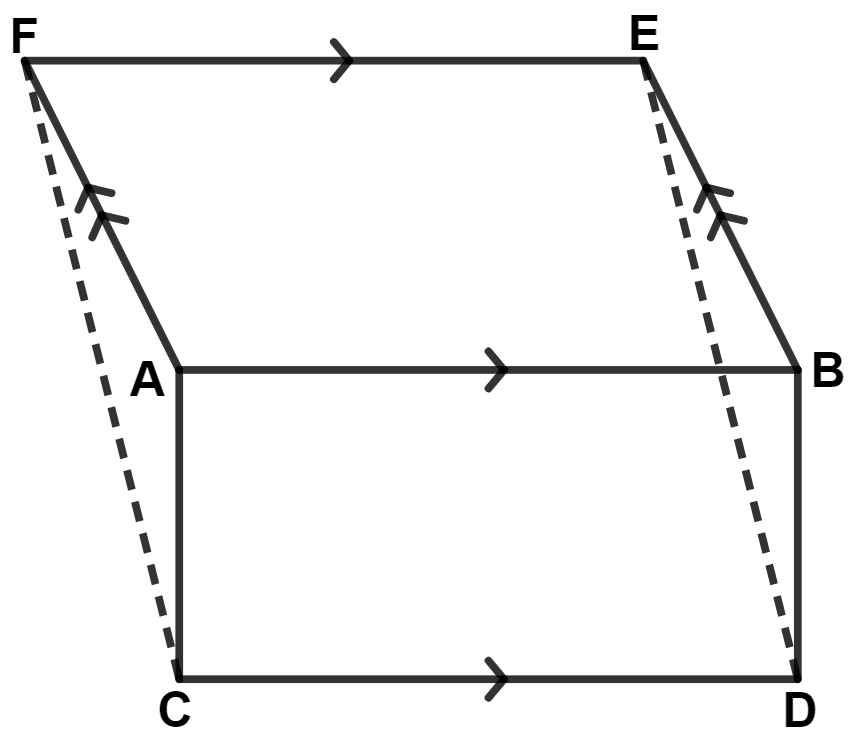
In the given figure, if area of triangle ADE is 60 cm2; state, giving reason, the area of :
(i) parallelogram ABED;
(ii) rectangle ABCF;
(iii) triangle ABE.
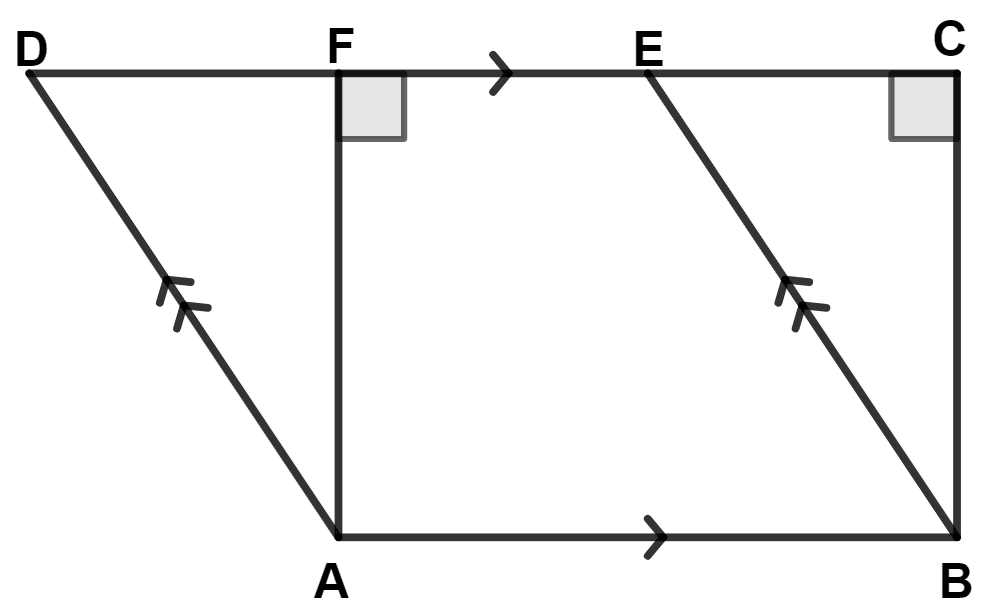
The given figure shows a rectangle ABDC and a parallelogram ABEF; drawn on opposite sides of AB. Prove that :
(i) quadrilateral CDEF is a parallelogram
(ii) Area of quad. CDEF = Area of rect. ABDC + Area of // gm ABEF