Mathematics
In triangle ABC, bisector of angle BAC meets opposite side BC at point D. If BD = CD, prove that △ ABC is isosceles.
Answer
Produce AD upto E such that AD = DE.
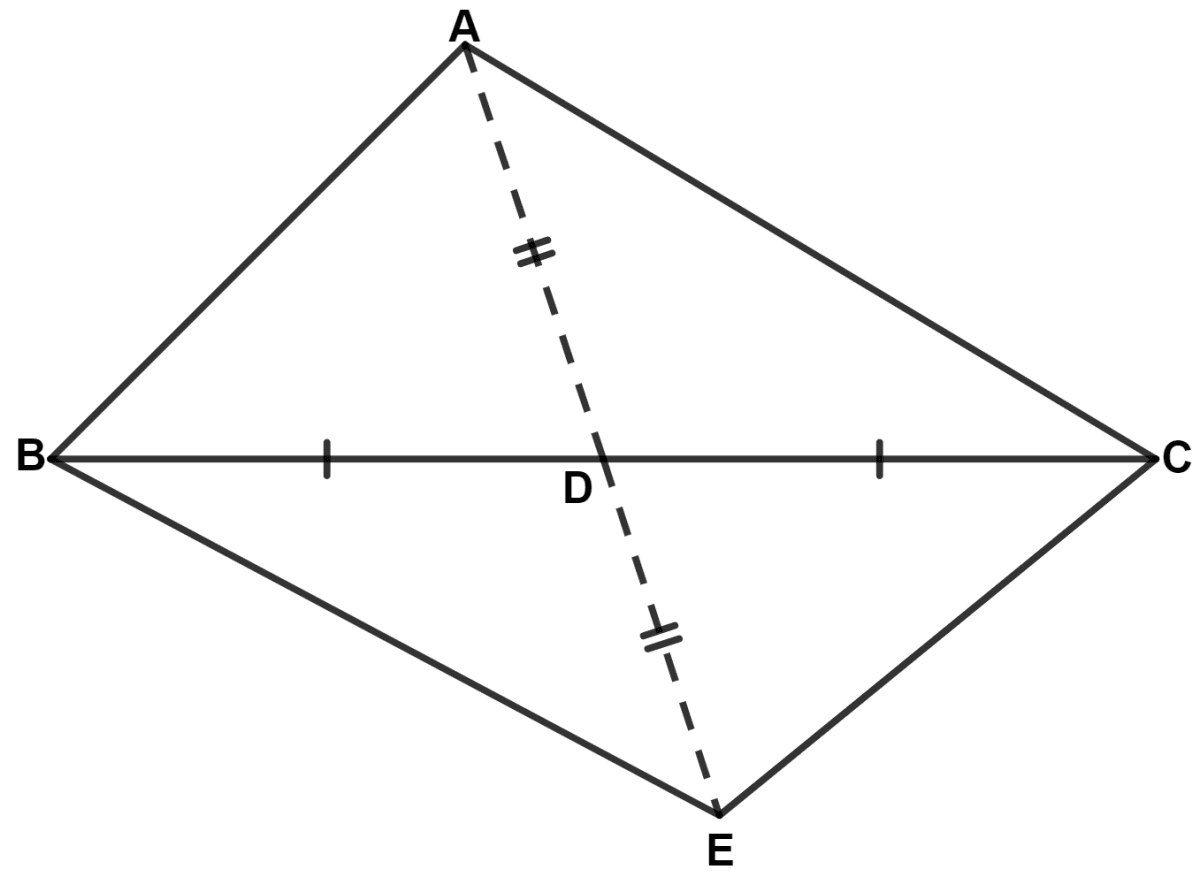
In △ ABD and △ EDC,
⇒ AD = DE (Given)
⇒ BD = CD (Given)
⇒ ∠ADB = ∠EDC (Vertically opposite angles are equal)
∴ △ ABD ≅ △ EDC (By S.A.S. axiom)
We know that,
Corresponding parts of congruent triangle are equal.
⇒ AB = CE ………(1)
⇒ ∠BAD = ∠CED
⇒ ∠BAD = ∠CAD (As AD is the bisector BAC)
∴ ∠CAD = ∠CED
∴ CE = AC (Sides opposite to equal angles are equal) ……….(2)
From equations (1) and (2), we get :
⇒ AB = AC.
Hence, proved that ABC is an isosceles triangle.
Related Questions
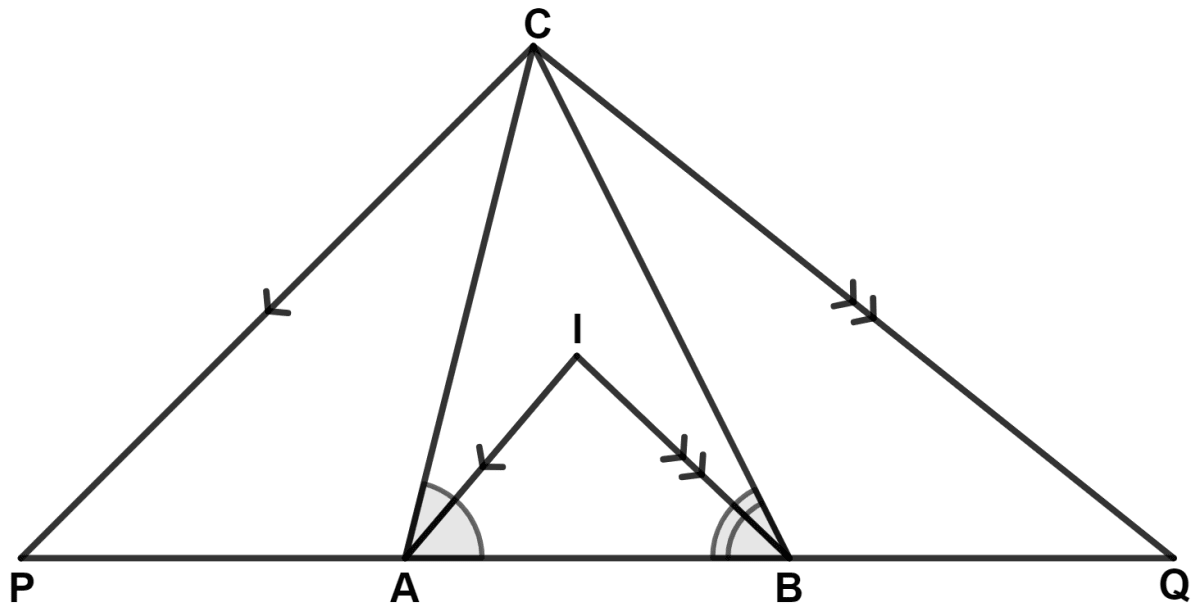
In the following figure; IA and IB are bisectors of angles CAB and CBA respectively. CP is parallel to IA and CQ is parallel to IB.
Prove that :
PQ = The perimeter of Δ ABC.
In the given figure; AB = BC and AD = EC. Prove that : BD = BE.
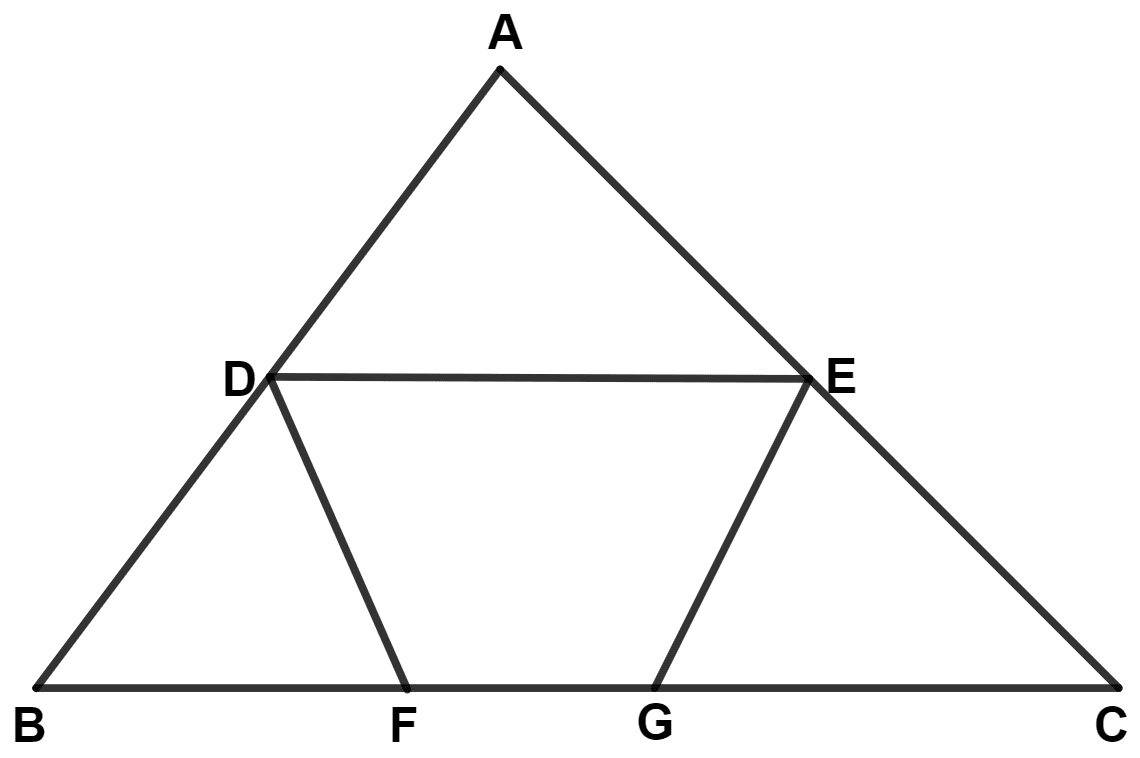
The given figure shows an equilateral triangle ABC with each side 15 cm. Also DE // BC, DF // AC and EG //AB. If DE + DF + EG = 20 cm, find FG.
In Δ ABC, D is a point on BC such that AB = AD = BD = DC. Show that :
∠ADC : ∠C = 4 : 1.
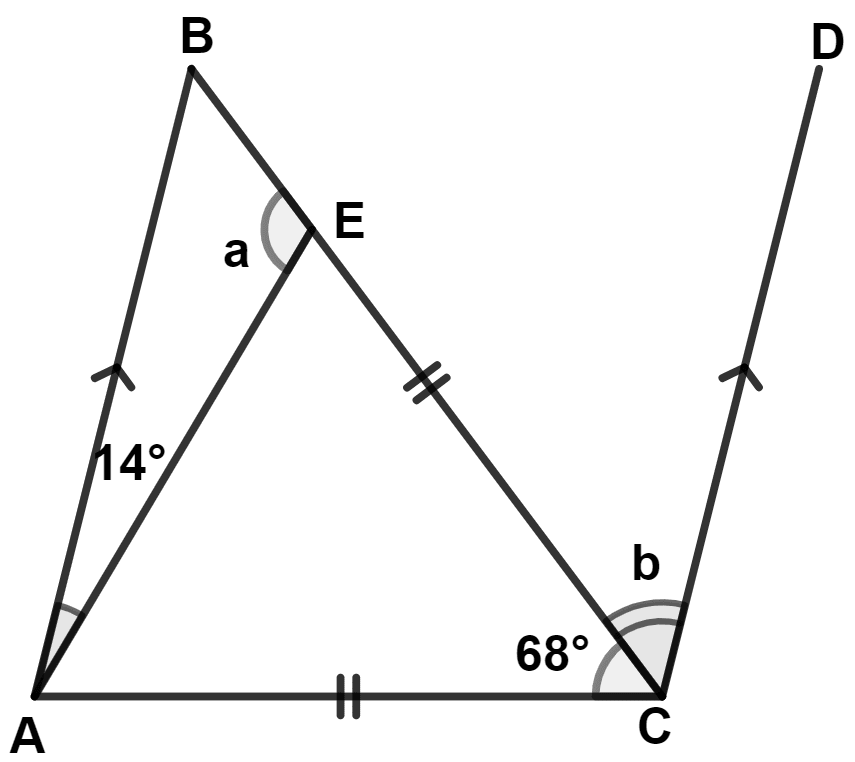
Using the information, given in each of the following figures, find the values of a and b.