Physics
A nichrome wire X with length (l) & cross-sectional area (A) is connected to a 10 V source and another nichrome wire Y with length (2l) & cross-sectional area (A/2), is connected to a 20 V source.
(a) Compare the resistances of wires X and Y. [Given that the resistivity of nichrome is (ρ).]
(b) Compare the electrical power consumed by each wire.
(c) Compare the masses of these wires. (Given that the density of nichrome is d.)
(d) State True or False : Wire X and wire Y both show the same rise in temperature in the same time.
Current Electricity
8 Likes
Answer
Given,
- Length of nichrome wire X (lX) = l
- Cross-sectional area of nichrome wire X (AX) = A
- Potential difference across nichrome wire X (VX) = 10 V
- Length of nichrome wire Y (lY) = 2l
- Cross-sectional area of nichrome wire Y (AY) = A/2
- Potential difference across nichrome wire Y (VY) = 20 V
- resistivity of nichrome = ρ
(a) Let 'RX' and 'RY' be the resistance of nichrome wire X and Y respectively.
Now,
And
As,
So, RX : RY = 1 : 4
(b)
And
So, PX : PY = 1 : 1
(c) Given,
Mass density of nichrome = d
Then,
Mass of wire X (mX) = d x volume = d x Al
And,
Mass of wire Y (mY) = d x volume = d x 2l x = d x Al = mX
So, mX : mY = 1 : 1
(d) True.
Reason —
Let, heat gained by the wire X be 'QX' and change in temperature be 'ΔTX'. Similarly, heat gained by the wire Y be 'QY' and change in temperature be 'ΔTY'.
Again, let specific heat capacity of nichrome be 'c' and same time be 't'.
Then,
QX = PX x t = mXc x ΔTX
and
QY = PY x t = mYc x ΔTY
As, PX = PY then QX = QY for same time t.
⇒ mXc x ΔTX = mYc x ΔTY
⇒ mX x ΔTX = mY x ΔTY
So,
ΔTX : ΔTY = mX : mY = 1 : 1
Hence, wire X and wire Y both show the same rise in temperature in the same time.
Answered By
6 Likes
Related Questions
The circuit depicted in the figure is employed for studying Ohm's Law. Instead of using a standard resistor, a student opts for a glass tube filled with mercury (tube 1), connected to the circuit through two electrodes E1 & E2. He records the readings of the ammeter and voltmeter, thereby calculates the resistance. The student repeats the experiment by substituting tube 1 with tube 2, where the same amount of mercury fills the tube 2.
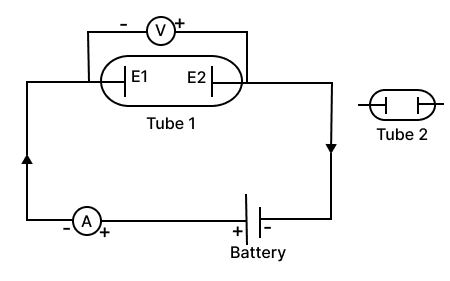
Neglecting internal resistance of the cell use (> or < or =) to compare
(a) the resistance in both the cases.
(b) the voltmeter readings in both the cases.
(c) the specific resistance in both the cases.
An appliance with a metal covering, rated at 2 kW, 220 V, is to be connected in a circuit. Given below are four diagrams (P, Q, R & S) depicting different circuit configurations.

(a) Identify the safest circuit.
(b) Write two reasons, supported by mathematical calculations, where applicable, to justify your choice.
Three bulbs of powers P1, P2 and P3 (P1 < P2 < P3) are connected in a certain way that P3 glows brightest.
(a) What type of connection exists between these bulbs?
(b) Compare the voltage across these bulbs. (Use >, < or =)
(c) Will the circuit still function if one of the bulbs is fused?
The given diagram shows the output of an AC generator. If the speed of the generator coil is doubled, then:

(a) what is the effect on the physical quantity indicated by ‘a’?
(b) what is the effect on the physical quantity indicated as ‘b’?
(c) give reason for your answer in (b).