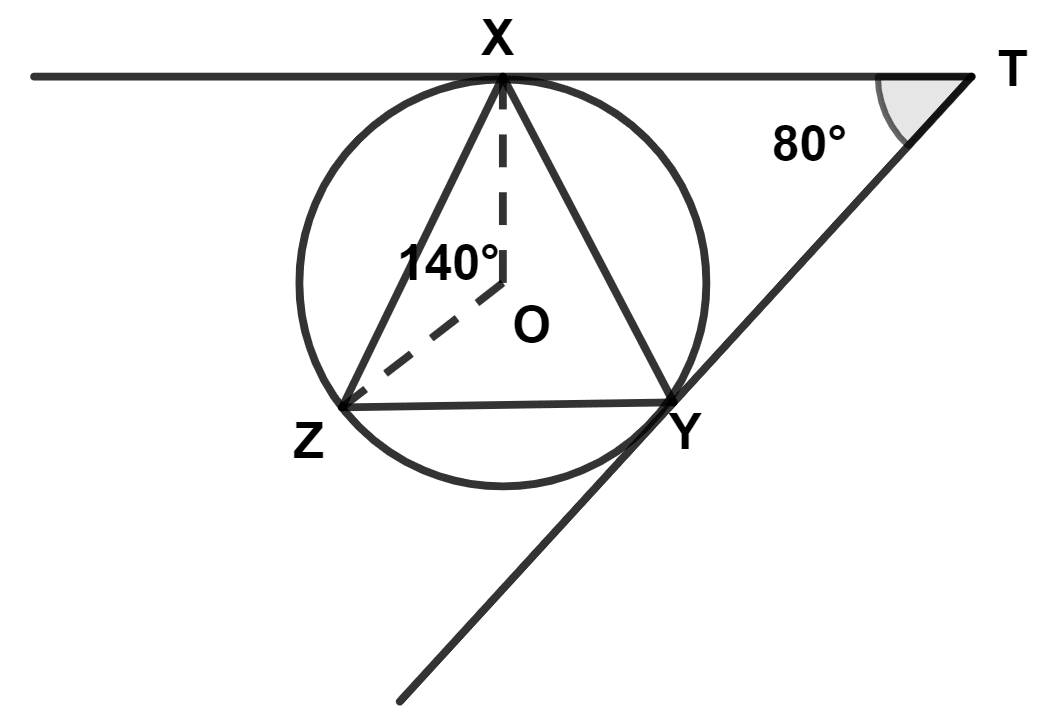
O is the center of the circumcircle of △ XYZ. Tangents at points X and Y meet each other at point T. If ∠XOZ = 140° and angle XTY = 80°, find angle ZXY.

We know that,

Tangents to a circle from a point are equal in length.

In △ XTY,

⇒ TX = TY

⇒ ∠TXY = ∠TYX = a (let) [Angles opposite to equal sides in a triangle are equal]

By angle sum property of triangle,

⇒ ∠TXY + ∠TYX + ∠XTY = 180°

⇒ a + a + 80° = 180°

⇒ 2a = 180° - 80°

⇒ 2a = 100°

⇒ a = $\dfrac{100°}{2}$ = 50°

⇒ ∠TXY = 50°.

In △ XOZ,

⇒ OZ = OX

⇒ ∠OXZ = ∠OZX = b (let) [Angles opposite to equal sides in a triangle are equal]

By angle sum property of triangle,

⇒ ∠OZX + ∠OXZ + ∠ZOX = 180°

⇒ b + b + 140° = 180°

⇒ 2b = 180° - 140°

⇒ 2b = 40°

⇒ b = $\dfrac{40°}{2}$ = 20°

⇒ ∠OXZ = 20°.

From figure,

⇒ ∠OXT = 90° [The tangent at any point of a circle is perpendicular to the radius through the point of contact.]

⇒ ∠ZXY = ∠OXZ + ∠OXT - ∠TXY

⇒ ∠ZXY = 20° + 90° - 50° = 60°.

Hence, ∠ZXY = 60°.