Physics
An object is placed at a distance of 10 cm from a convex lens of focal length 20 cm.
(a) Find the position of the image.
(b) What is the nature of the image?
Refraction Lens
5 Likes
Answer
Given,
- Object distance (u) = - 10 cm
- Focal Length (f) = + 20 cm
Let, image distance be 'v'.
From lens formula,
So, the image will form at a distance of 20 cm in front of the convex lens.
(b) As,
Here, sign of magnification is positive implying virtual and erect image formation and since magnification is 2 so size of the image is 2 times the size of the object.
Hence, formed images is virtual, erect and 2 times the size of the object.
Answered By
4 Likes
Related Questions
Answer the following with respect to a concave lens (L).
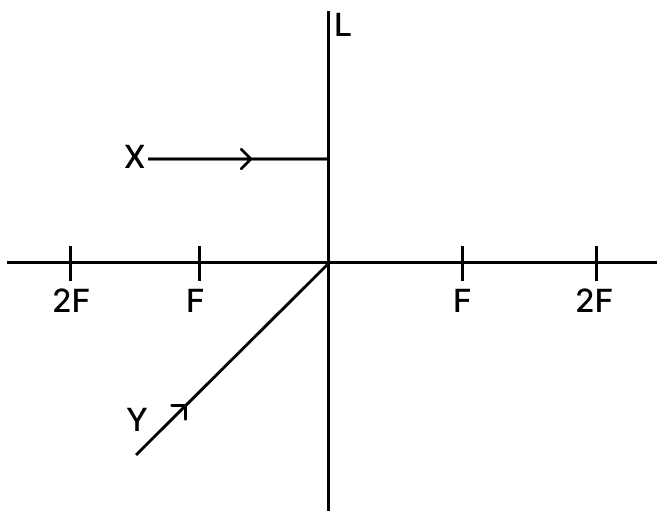
(a) Describe the path of the rays X and Y through the lens.
(b) Give one use of this lens.
(c) Calculate its power if the focal length of this lens is 20 cm.
The diagram given below shows a triangular prism of a certain material with fluorescent screen placed adjacent to it. The yellow light ray striking the surface ST of the prism shows a fluorescent spot at point X.
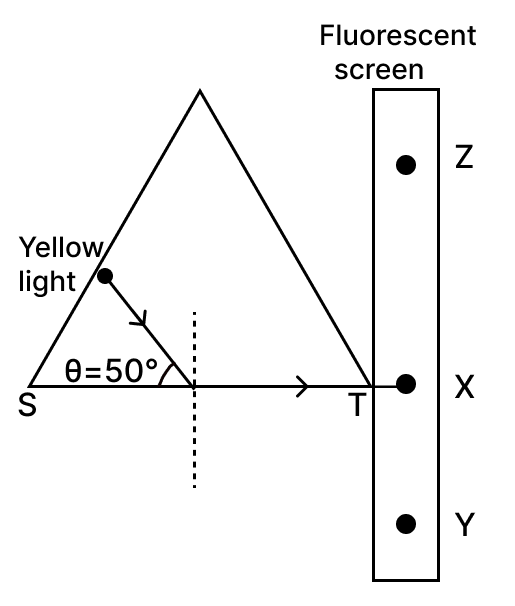
(a) Calculate the critical angle of the material of the prism for yellow colour.
(b) To move the fluorescent spot towards Y, the value of θ should be …………… [> 50, < 50 or = 50].
(c) Which direction will the florescent spot move if yellow light is replaced with indigo light? (towards Y or towards Z)
(a) Name the electromagnetic radiations which are used for sterilising water in a water purifier.
(b) State any one property of the radiations mentioned by you in part (a).
(c) Why are the danger signals red in colour?
A uniform metre ruler is balanced horizontally on a knife edge placed at 60 cm mark when a mass m is suspended from 75 cm mark. Draw the diagram of the arrangement. State with reason (through mathematical steps) whether the mass of the scale is greater than, less than or equal to the mass m?