In a pentagon ABCDE, DP is drawn perpendicular to AB and is perpendicular to CE also at point Q. If AP = BP = 12 cm, EQ = CQ = 8 cm, DE = DC = 10 cm and DP = 18 cm, find the area of the pentagon ABCDE.

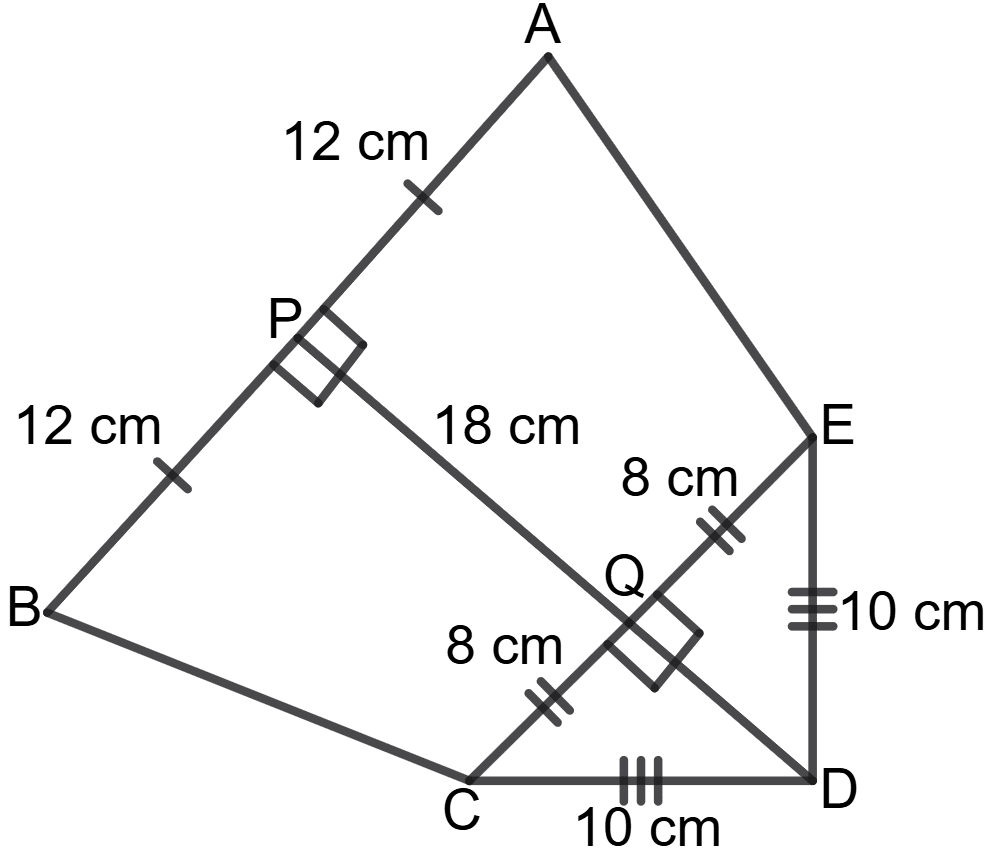
Given: DP ⊥ AB at point P, with AP = BP = 12 cm, so AB = 24 cm.

DP ⊥ CE at point Q, with EQ = CQ = 8 cm, so CE = 16 cm.

DE = DC = 10 cm

DP = 18 cm

In triangle DEQ, using pythagoras theorem,

⇒ DE² = EQ² + DQ²

⇒ 10² = 8² + h²

⇒ h² = 100 - 64

⇒ h² = 36

⇒ h = $\sqrt{36}$

⇒ h = $\pm$ 6

Since height cannot be negative, QD = 6 cm.

PQ = PD - QD = 18 - 6 = 12 cm

From the figure, the pentagon ABCDE is composed of: trapezium ABCE and triangle CDE.

Area of trapezium ABCE = $\dfrac{1}{2}$ × (Sum of parallel sides) × height

= $\dfrac{1}{2}$ × (AB + CE) × PQ

= $\dfrac{1}{2}$ × (24 + 16) × 12

= 40 x 6

= 240 cm²

Area of △ CDE = $\dfrac{1}{2}$ × base × height

= $\dfrac{1}{2}$ × 16 × 6

= 8 × 6

= 48 cm²

Total Area of Pentagon ABCDE = Area trapezium ABCE + Area △ CDE = 240 + 48 = 288 cm²

Hence, the area of pentagon ABCDE = 288 cm².