JOIN NOW

Mathematics

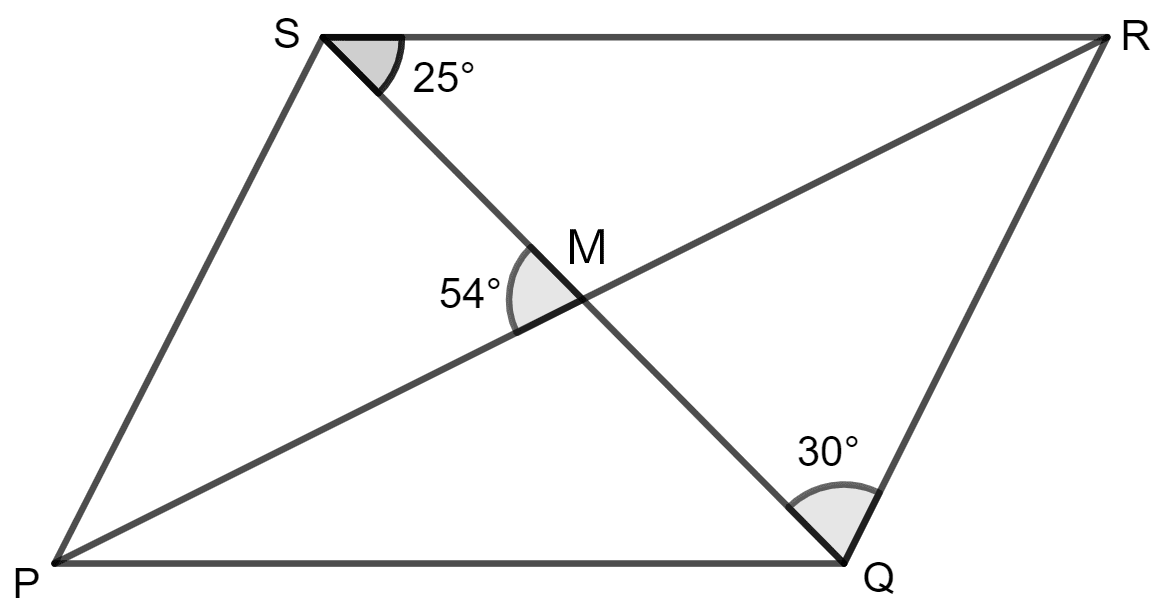
PQRS is a parallelogram whose diagonals intersect at M.

If ∠PMS = 54°, ∠QSR = 25° and ∠SQR = 30°, find :

(i) ∠RPS

(ii) ∠PRS

(iii) ∠PSR.

Quadrilaterals

12 Likes

Answer

(i) PQRS is a parallelogram which means opposite sides are parallel.

PQRS is a parallelogram whose diagonals intersect at M. Special Types of Quadrilaterals, Concise Mathematics Solutions ICSE Class 8.

When QR is parallel to PS.

⇒ ∠PSQ = ∠SQR (alternate angles)

It is given that ∠PMS = 54°, ∠QSR = 25° and ∠SQR = 30°

So, ∠PSQ = ∠SQR = 30°

In triangle SMP, sum of all the angles of triangle is = 180°

⇒ ∠PMS + ∠PSM + ∠MPS = 180°

(As we know , ∠MPS = ∠RPS)

⇒ 54° + 30° + ∠RPS = 180°

⇒ 84° + ∠RPS = 180°

⇒ ∠RPS = 180° - 84°

⇒ ∠RPS = 96°

Hence, the value of ∠RPS is 96°.

(ii) Now, consider triangle MSR, according to exterior angle property, exterior angle is equals to sum of two opposite interior angles.

∠MRS + ∠RSM = ∠PMS

⇒ ∠PRS + 25° = 54°

⇒ ∠PRS = 54° - 25°

⇒ ∠PRS = 29°

Hence, the value of ∠PRS is 29°.

(iii) ∠PSR is divided into two angles ∠PSQ and ∠RSQ. So,

∠PSR = ∠PSQ + ∠RSQ

= 30° + 25°

= 55°

Hence, the value of ∠PSR is 55°.

Answered By

6 Likes

Related Questions