Mathematics
Prove that the median drawn from the vertex P of an isosceles triangle △PQR with PQ = PR is perpendicular to QR and bisects ∠P.
Related Questions
In the adjoining figure, AB = CD, CE = BF and ∠ACE = ∠DBF. Prove that
(i) △ACE ≅ △DBF
(ii) AE = DF.

Two line segments AC and BD bisect each other at P. Draw the diagram and prove that
(i) AB = CD
(ii) ∠BAC = ∠DCA
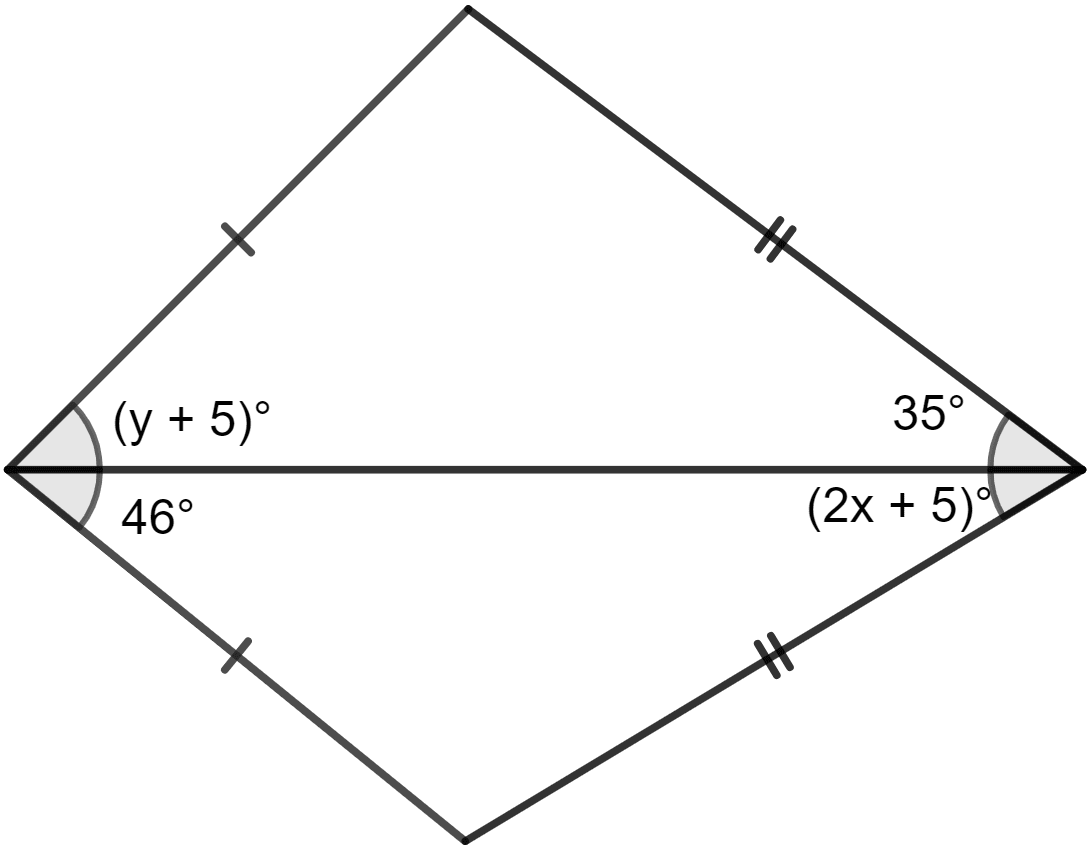
In the adjoining figure, find the values of x and y.
In triangles ABC and PQR, ∠A = ∠Q and ∠B = ∠R. Which side of △PQR should be equal to side AB of △ABC so that the two triangles are congruent? Give reason for your answer.