Mathematics
State for each of the following statements whether it is true or false :
(a) If (x - a)(x - b) < 0, then x < a and x < b.
(b) If a < 0 and b < 0, then (a + b)2 > 0.
(c) If a and b are any two integers such that a > b, then a2 > b2.
(d) If p = q + 2, then p > q.
(e) If a and b are two negative integers such that a < b, then
Linear Inequations
10 Likes
Answer
(a) False
Reason — If x < a and x < b, then (x - a)(x - b) will be greater than 0 as multiplication of two negative number generates a positive number.
(b) True
Reason — If a < 0 and b < 0, then (a + b) will be a negative number and square of any negative number is greater than 0, so (a + b)2 is greater than 0.
(c) False
Reason — If a > b, then a2 > b2 is true only if a and b are positive numbers.
(d) True
Reason — If a positive number is added to any number (suppose x), then resultant number is greater than x.
(e) False
Reason — If, a < b and both are two negative integers then on recripocating the numbers the sign will be reversed, so .
Answered By
6 Likes
Related Questions
The given diagram represents two sets A and B on real number lines.
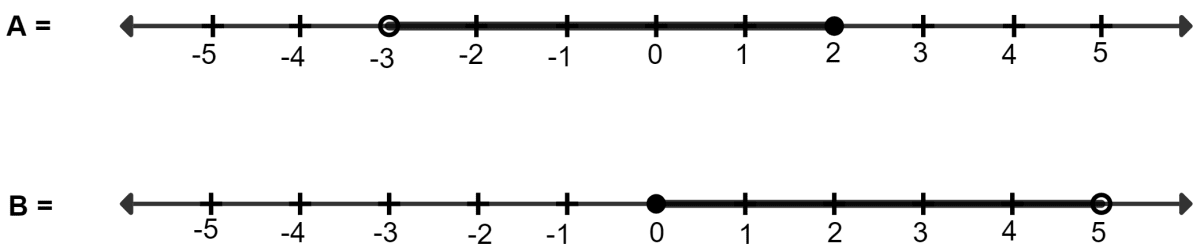
(i) Write down A and B in set-builder form.
(ii) Represent A ∪ B, A ∩ B, A' ∩ B, A - B and B - A on separate number lines.
Find the values of x, which satisfy the inequation :
; x ∈ N
Graph the solution set on the real number line.

Given 20 - 5x < 5(x + 8), find the smallest value of x when :
(i) x ∈ I
(ii) x ∈ W
(iii) x ∈ N
If x ∈ Z, solve : 2 + 4x < 2x - 5 ≤ 3x. Also, represent its solution on the real number line.