Mathematics
Statement 1: Each side of a cuboid is doubled, its total surface area is also doubled.
Statement 2: The surface area of resulting cuboid is 2 x 2 x 2 times the original area.
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Mensuration
1 Like
Answer
Let the original cuboid have length l, breadth b, and height h.
So, sides of new cuboid = 2l, 2b and 2h.
As we know that surface area of the cuboid = 2(lb + bh + hl)
The surface area of new cuboid = 2[(2l) x (2b) + (2b) x (2h) + (2h) x (2l)]
= 2(4lb + 4bh + 4hl)
= 2 x 2 x [2(lb + bh + hl)]
= 4 x surface area of the cuboid
= 2 x 2 x surface area of the cuboid
∴ Both the statements are false.
Hence, option 2 is the correct option.
Answered By
1 Like
Related Questions
The diameters of two solid spheres are in the ratio 5 : 7. The ratio between areas of their curved surfaces is :
5 : 7
7 : 5
49 : 25
25 : 49
The radius of a cylinder is doubled and its curved surface area is kept as same, the height of the cylinder is:
same
doubled
halved
none of these
Assertion (A): The radius of a hemisphere increases from r cm to 2r cm. The ratio between the surface area of the original hemisphere and the resulting hemisphere is 1 : 4.
Reason (R): Surface area of the first case = πr2 + 2πr2
Surface area of the second case = π(2r)2 + 2π(2r)2
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.
Assertion (A): A sphere is inscribed in a cylinder the ratio of the volume of the cylinder to the volume of the sphere is 1 : 4.
Reason (R): Required ratio = πr2 x 2r : πr3
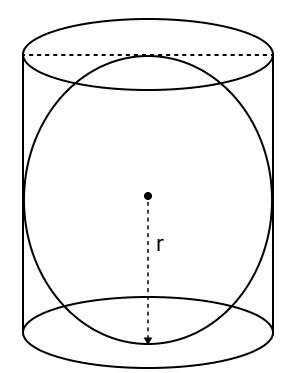
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.