Mathematics
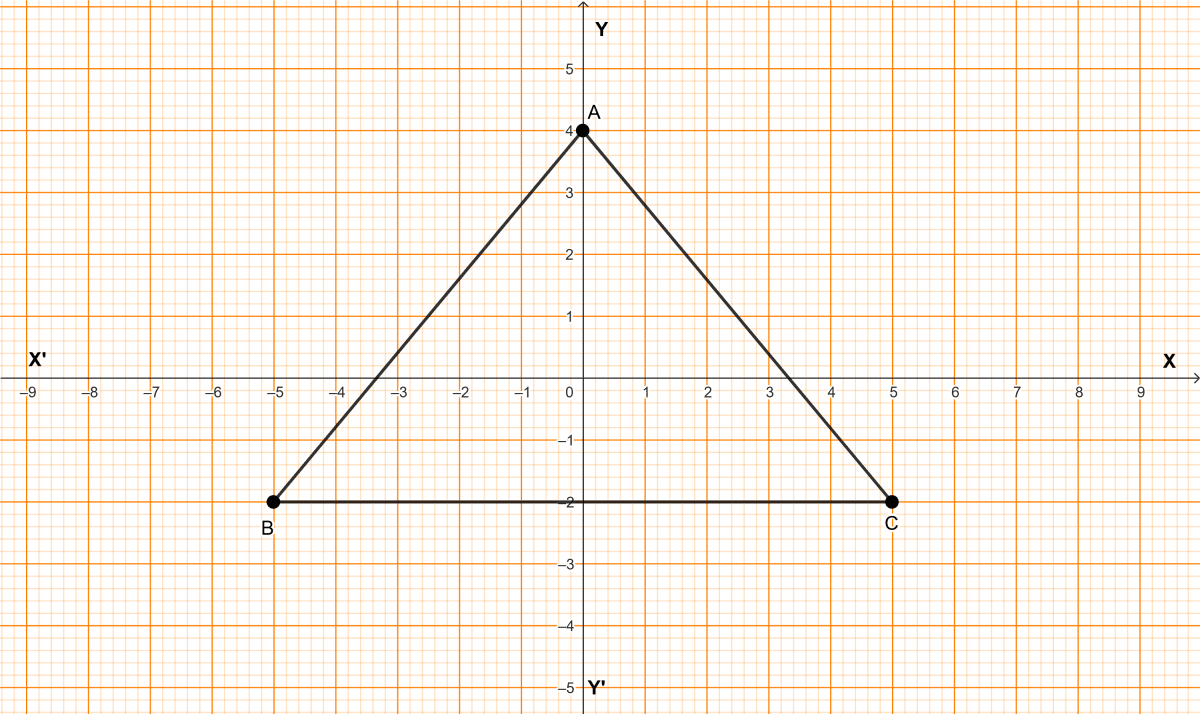
Study the graph and answer the following questions :
(a) Write down the co-ordinates of points A, B and C.
(b) Calculate the area of triangle ABC.
Related Questions
Use graph paper for this question. Take 2 cm = 1 unit along both the axes.
(i) Plot the points A(2, 3), B(2, 2) and C(3, 2).
(ii) Reflect A, B and C about x-axis and name them as A', B' and C' respectively.
(iii) Reflect A, B, C, A', B' and C' about y-axis and name them as A'', B'', C'', A''', B''' and C''' respectively.
(iv) Join A, B, C, C'', B'', A'', A''', B''', C''', C', B', A' and A to make a closed figure.
Plot points A(0, 3), B(4, 0), C(6, 2) and D(5, 0). Reflect the points as given below and write their coordinates :
(a) Reflect A on x-axis to A’.
(b) Reflect B on y-axis to B’.
(c) Reflect C on x-axis to C’.
(d) D remain invariant when reflected on the line whose equation is …………… .
(e) Join the points A, B, C, D, C’, B, A’, B’ and A to form a closed figure. Name the closed figure BCDC’.
Points (8, 0) and (-3, 0) are invariant points under reflection in the line L1, points (0, -9) and (0, 5) are invariant points under reflection in the line L2.
(i) Name or write down equations of the lines L1 and L2.
(ii) Write down the images of points P(3, 5) and Q(-8, 3) after reflection in line L1. Name the images as P' and Q' respectively.
(iii) Write down the images of P and Q on reflection in L2. Name the images as P" and Q" respectively.
(iv) Describe a single transformation that maps P' to P".