Points (8, 0) and (-3, 0) are invariant points under reflection in the line L₁, points (0, -9) and (0, 5) are invariant points under reflection in the line L₂.

(i) Name or write down equations of the lines L₁ and L₂.

(ii) Write down the images of points P(3, 5) and Q(-8, 3) after reflection in line L₁. Name the images as P' and Q' respectively.

(iii) Write down the images of P and Q on reflection in L₂. Name the images as P" and Q" respectively.

(iv) Describe a single transformation that maps P' to P".

(i) We know that,

Points are invariant in the line on which they lie.

Given,

(8, 0) and (-3, 0) are invariant points under reflection in the line L₁.

Points (8, 0) and (-3, 0) lie on x-axis.

∴ L₁ = x-axis.

(0, -9) and (0, 5) are invariant points under reflection in the line L₂.

Points (0, -9) and (0, 5) lie on y-axis.

∴ L₂ = y-axis.

Hence, L₁ = x-axis or y = 0 and L₂ = y-axis or x = 0.

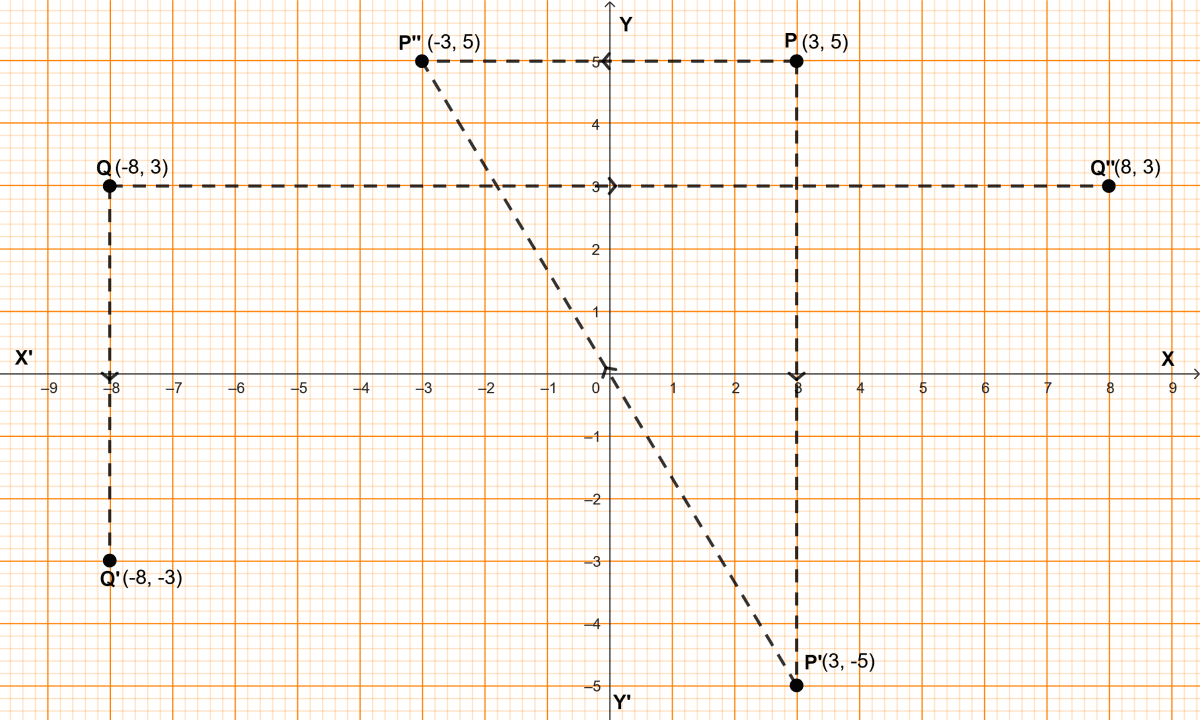
(ii) From graph,

Co-ordinates of P' = (3, -5) and Q' = (-8, -3).

(iii) From graph,

Co-ordinates of P" = (-3, 5) and Q" = (8, 3).

(iv) From graph,

The single transformation that maps P' to P" is reflecting in origin.