Mathematics
The altitude and the base of a triangular field are in the ratio 6 : 5. If its cost is ₹ 49,57,200 at the rate of ₹ 36,720 per hectare and 1 hectare = 10,000 sq.m, find (in metre) the dimensions of the field.
Area Trapezium Polygon
8 Likes
Answer
Given:
Ratio of altitude and base of the field = 6 : 5
Total cost = ₹ 49,57,200
Rate = ₹ 36,720 per hectare
As we know that area of the triangular field x rate = total cost
⇒ Area of the triangular field x = ₹ 49,57,200
⇒ Area of the triangular field = ₹
⇒ Area of the triangular field = ₹
⇒ Area of the triangular field = 13,50,000 m2
Let the altitude be 6a and the base be 5a.
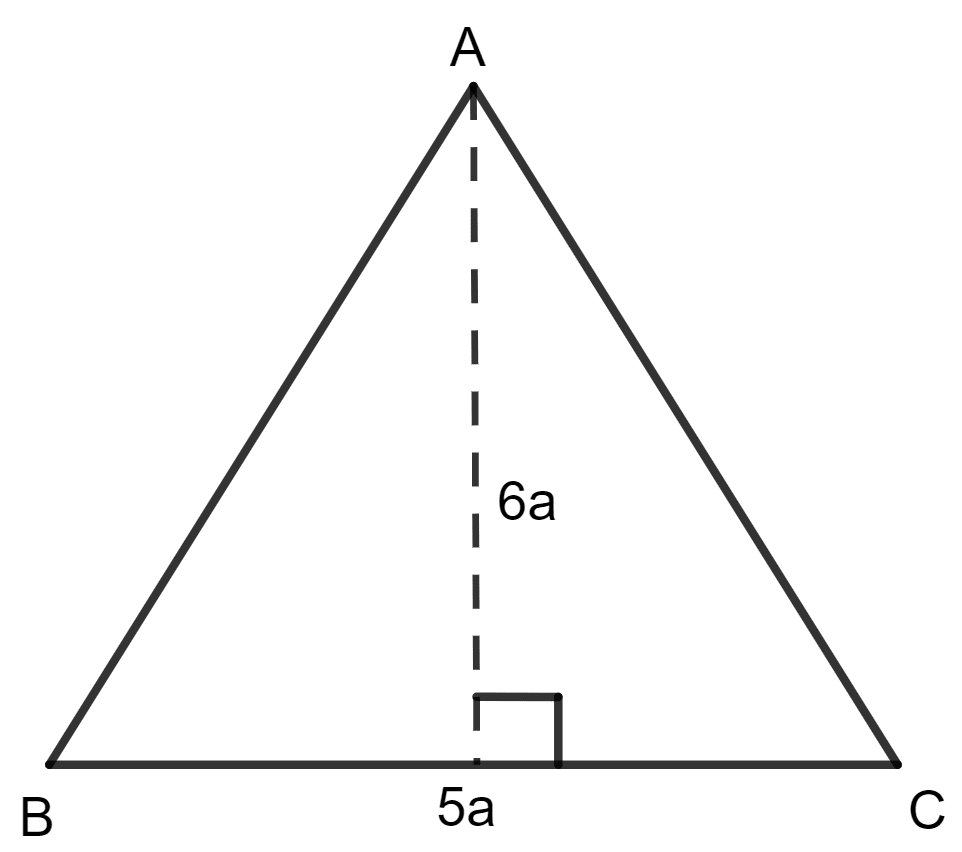
As we know, the area of a triangle = x base x height
⇒ 13,50,000 = x 6a x 5a
⇒ 13,50,000 = x 30a2
⇒ 13,50,000 = 15a2
⇒ a2 =
⇒ a2 = 90000
⇒ a =
⇒ a = 300
So, the altitude = 6a
= 6 x 300
= 1800 m
And, the base = 5a
= 5 x 300
= 1500 m
Hence, the dimensions of the field are 1800 m and 1500 m.
Answered By
5 Likes
Related Questions
The lengths of the sides of a triangle are in the ratio 4 : 5 : 3 and its perimeter is 96 cm. Find its area.
One of the equal sides of an isosceles triangle is 13 cm and its perimeter is 50 cm. Find the area of the triangle.
Find the area of the right-angled triangle with hypotenuse 40 cm and one of the other two sides 24 cm.
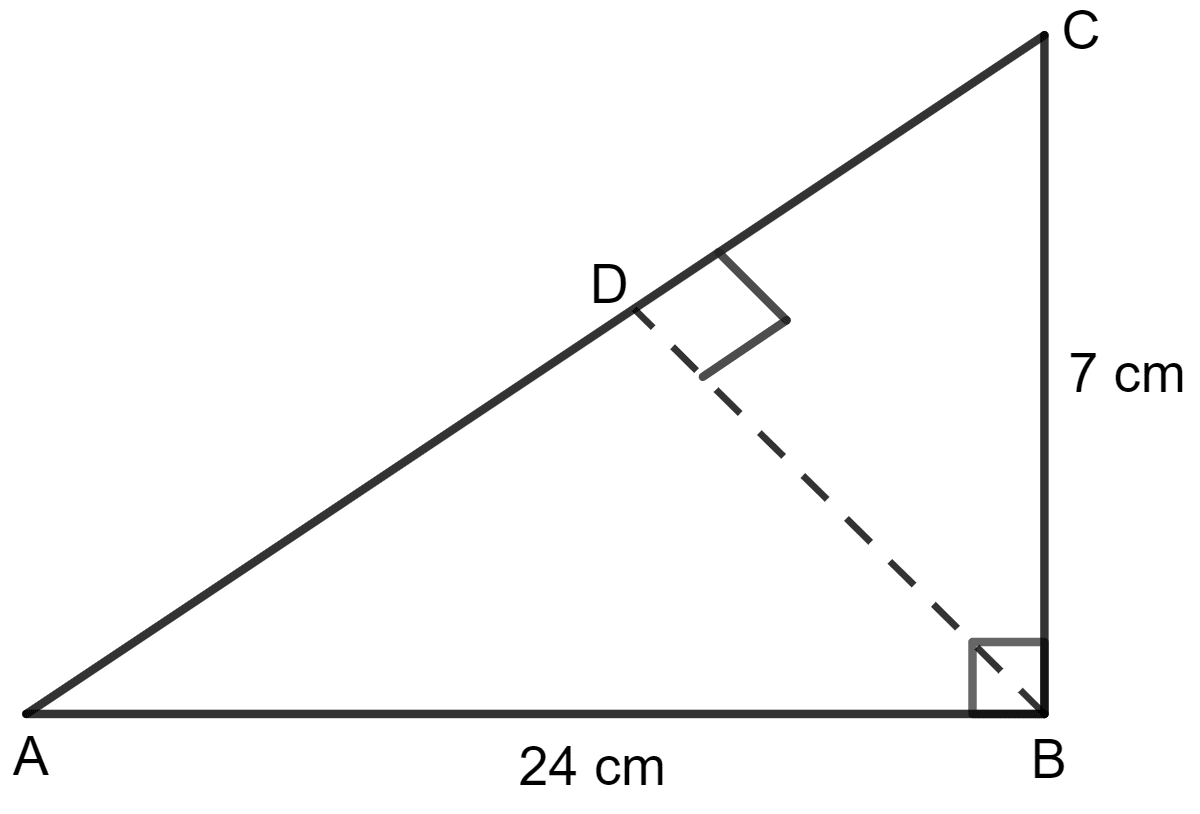
Use the information given in the given figure to find:
(i) the length of AC.
(ii) the area of △ ABC.
(iii) the length of BD, correct to one decimal place.