Mathematics
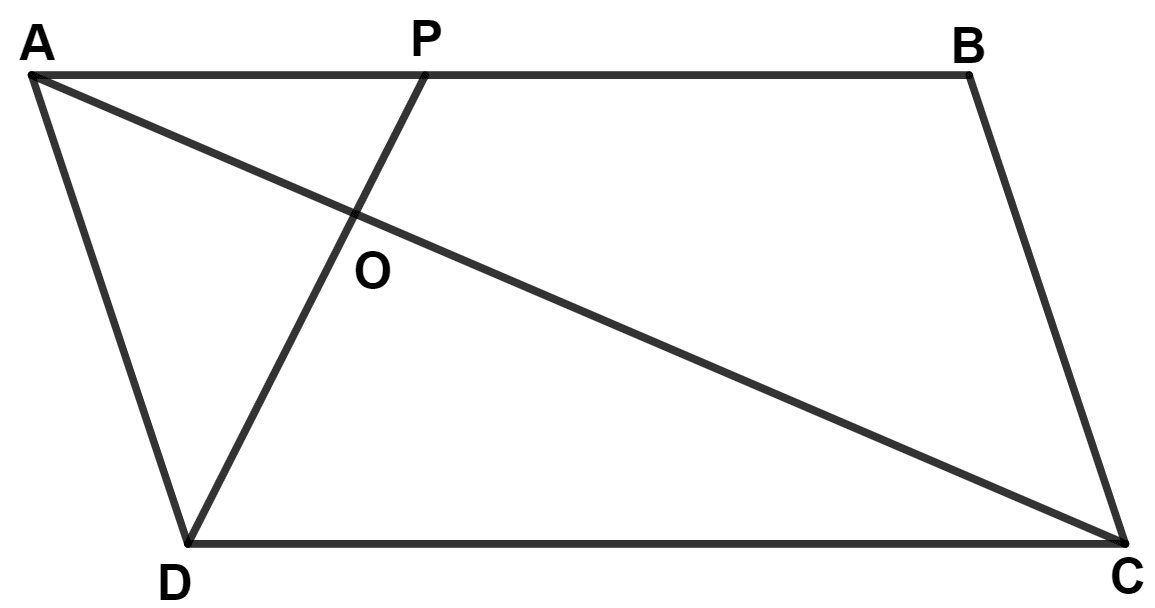
The given figure shows a parallelogram ABCD with area 324 sq.cm. P is a point in AB such that AP : PB = 1 : 2. Find the area of △ APD.
Theorems on Area
9 Likes
Answer
Join BD.
We know that,
Ratio of the area of triangles with same vertex and bases along the same line is equal to the ratio of their respective bases.
We know that,
The area of triangle is half that of a parallelogram on the same base and between the same parallels.
△ ABD and || gm ABCD lie on same base AB and between same parallel lines AB and DC.
∴ Area of △ ABD = Area of || gm ABCD = = 162 cm2.
From figure,
⇒ Area of △ ABD = Area of △ APD + Area of △ BPD
⇒ 162 = Area of △ APD + 2 Area of △ APD
⇒ 3 Area of △ APD = 162
⇒ Area of △ APD = = 54 cm2.
Hence, area of △ APD = 54 cm2.
Answered By
7 Likes
Related Questions
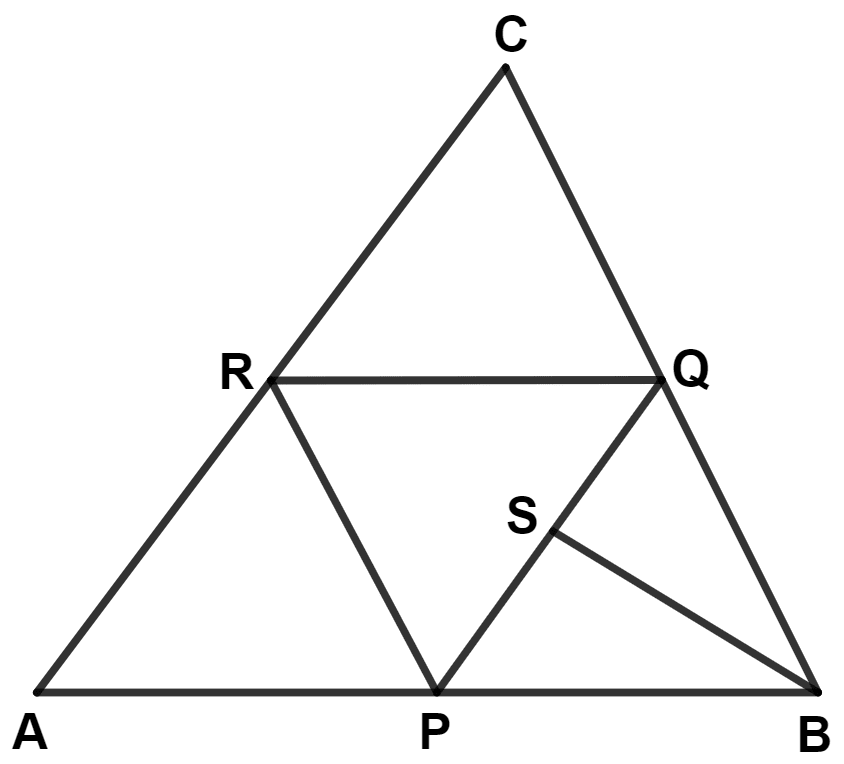
The following figure shows a triangle ABC in which P, Q and R are mid-points of sides AB, BC and CA respectively. S is mid-point of PQ. Prove that :
ar.(△ ABC) = 8 × ar.(△ QSB)
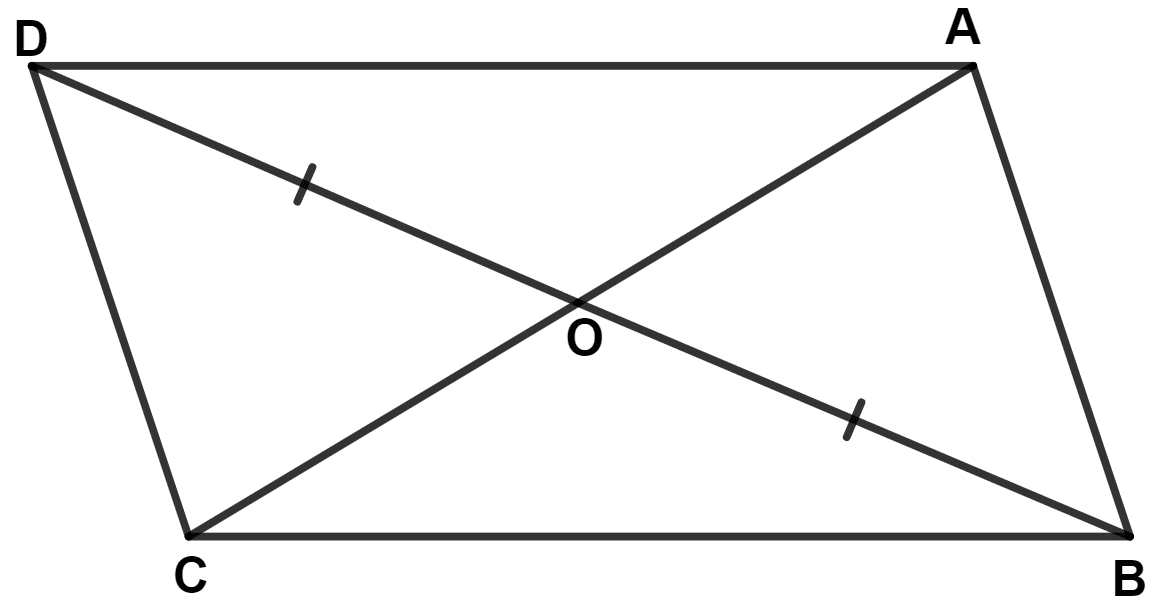
In the given figure, the diagonals AC and BD intersect at point O. If OB = OD and AB // DC, prove that :
(i) Area of (△ DOC) = Area of (△ AOB)
(ii) Area of (△ DCB) = Area of (△ ACB)
(iii) ABCD is a parallelogram.
In △ ABC, E and F are mid-points of sides AB and AC respectively. If BF and CE intersect each other at point O, prove that the △ OBC and quadrilateral AEOF are equal in area.
In parallelogram ABCD, P is mid-point of AB. CP and BD intersect each other at point O. If area of △ POB = 40 cm2 and OP : OC = 1 : 2, find :
(i) Areas of △ BOC and △ PBC
(ii) Area of △ ABC and parallelogram ABCD.