Mathematics
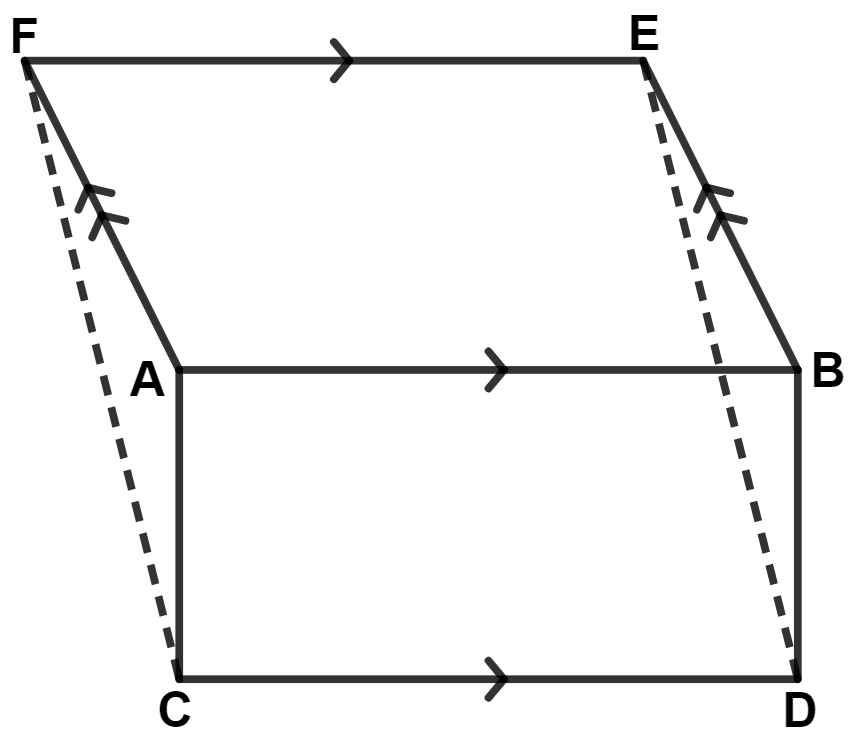
The given figure shows a rectangle ABDC and a parallelogram ABEF; drawn on opposite sides of AB. Prove that :
(i) quadrilateral CDEF is a parallelogram
(ii) Area of quad. CDEF = Area of rect. ABDC + Area of // gm ABEF
Theorems on Area
48 Likes
Answer
(i) Given,
ABCD is a rectangle.
∴ AB = CD (Opposite sides of rectangle are equal) ……………(1)
Given,
ABEF is a rectangle.
∴ AB = FE (Opposite sides of parallelogram are equal) ……………(2)
From equations (1) and (2), we get :
⇒ CD = FE.
From figure,
CD || FE
Since, one pair of opposite sides of quadrilateral CDEF are equal and parallel.
∴ CDEF is a parallelogram.
Hence, proved that CDEF is a parallelogram.
(ii) In △ AFC and △ BED,
⇒ AF = BE (Opposite sides of parallelogram ABEF)
⇒ AC = BD (Opposite sides of rectangle ABCD)
⇒ CF = ED (Opposite sides of parallelogram CDEF)
∴ △ AFC ≅ △ BED (By S.S.S. axiom)
We know that,
Area of congruent triangle are equal.
∴ Area of △ AFC = Area of △ BED ……….(1)
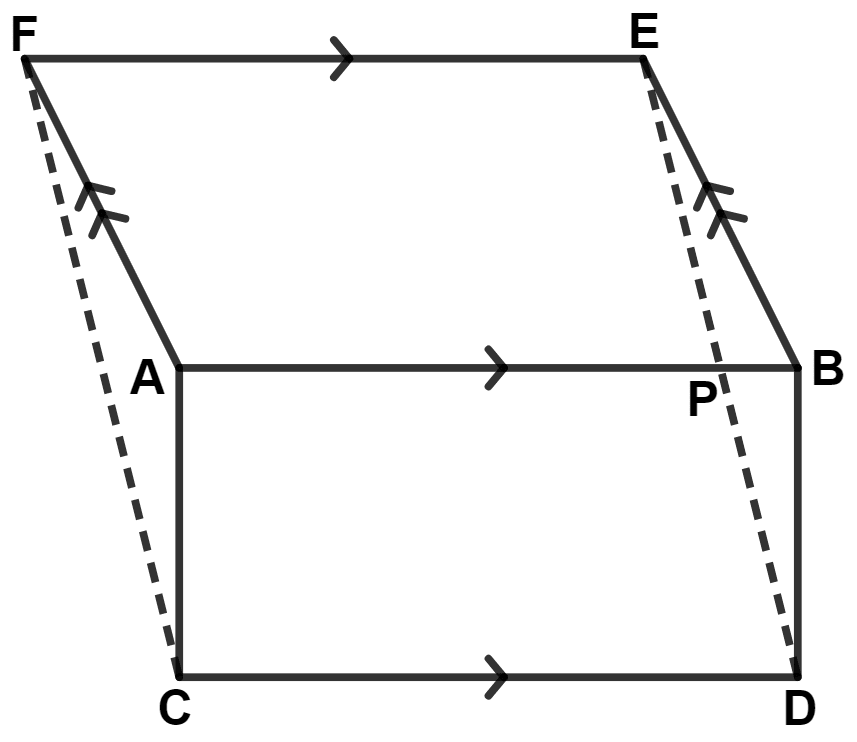
From figure,
⇒ Area of quadrilateral CDEF = Area of △ ACF + Area of ACDPEF
⇒ Area of quadrilateral CDEF = Area of △ BED + Area of ACDPEF [From equation (1)]
⇒ Area of quadrilateral CDEF = Area of CDBEPA
⇒ Area of quadrilateral CDEF = Area of rect. ABDC + Area of // gm ABEF.
Hence, proved that Area of quadrilateral CDEF = Area of rect. ABDC + Area of // gm ABEF.
Answered By
34 Likes
Related Questions
In the given figure, D is mid-point of side BC, the area of triangle BEA is equal to area of triangle :
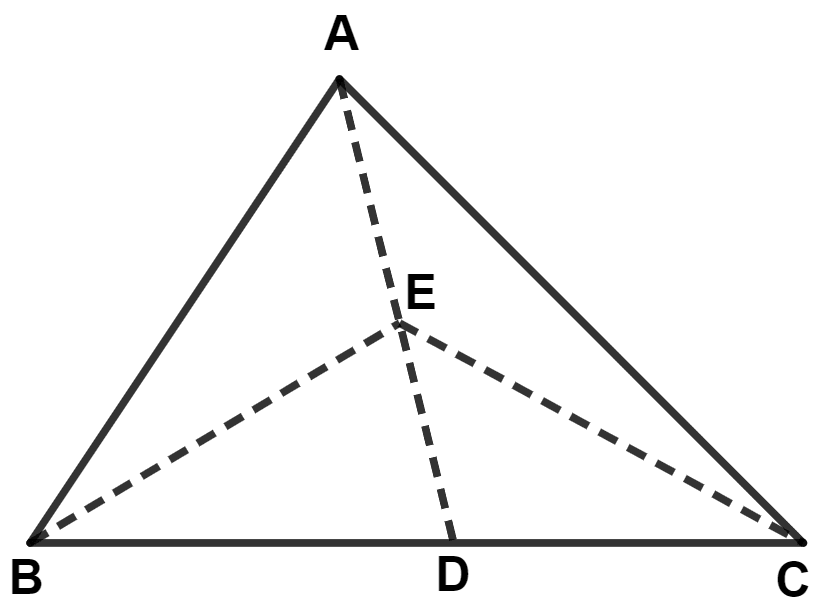
BED
CED
CEA
ACD
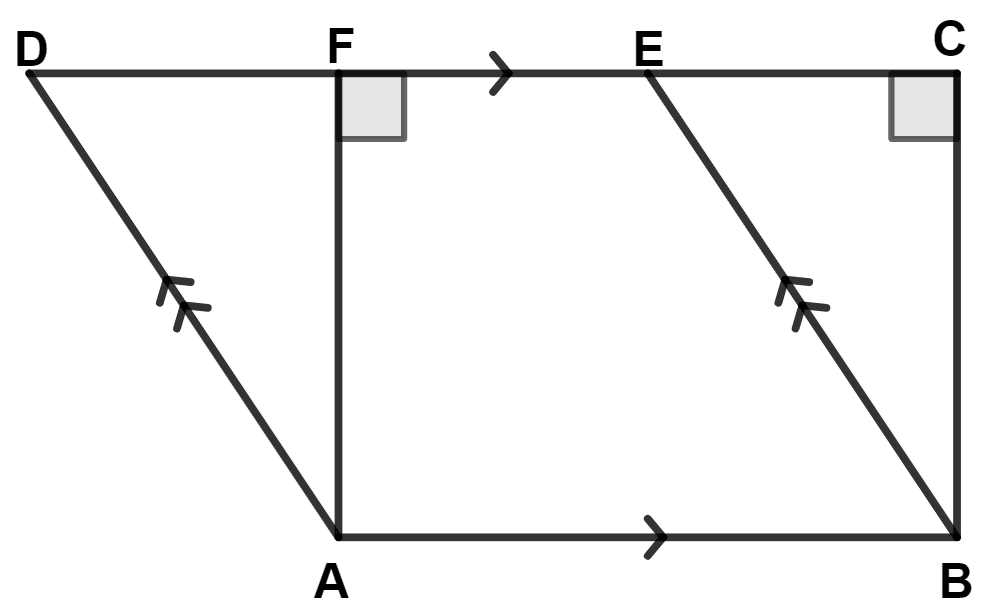
In the given figure, if area of triangle ADE is 60 cm2; state, giving reason, the area of :
(i) parallelogram ABED;
(ii) rectangle ABCF;
(iii) triangle ABE.
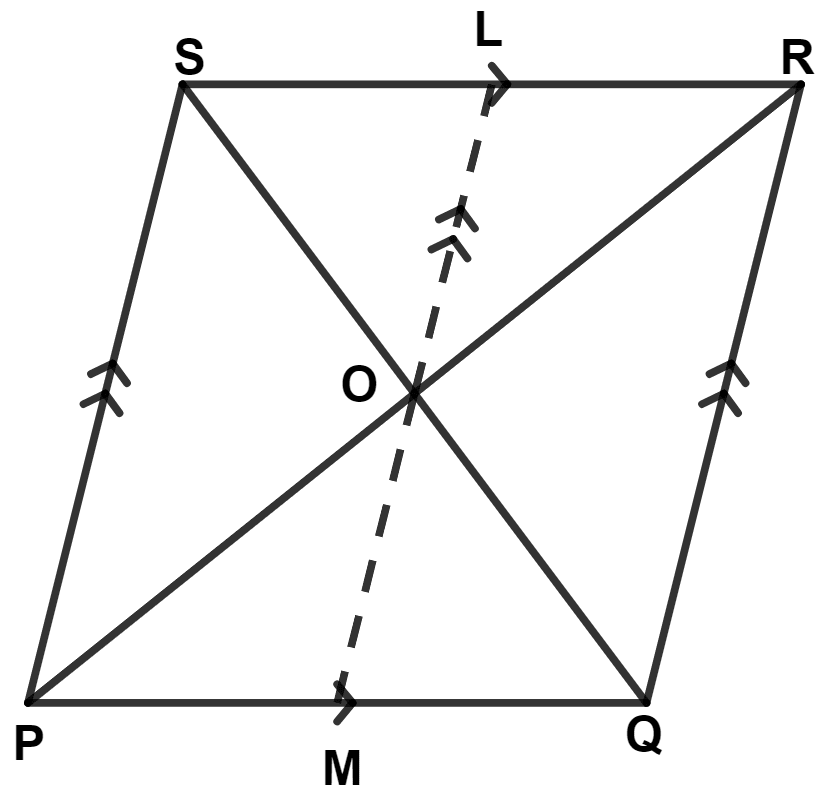
In the given figure, diagonals PR and QS of the parallelogram PQRS intersect at point O and LM is parallel to PS. Show that :
(i) 2 Area (△ POS) = Area (// gm PMLS)
(ii) Area (△ POS) + Area (△ QOR) = Area (//gm PQRS)
(iii) Area (△ POS) + Area (△ QOR) = Area (△ POQ) + Area (△ SOR)
In parallelogram ABCD, P is a point on side AB and Q is a point on side BC. Prove that :
(i) △ CPD and △ AQD are equal in area.
(ii) Area (△ AQD) = Area (△ APD) + Area (△ CPB)