Mathematics
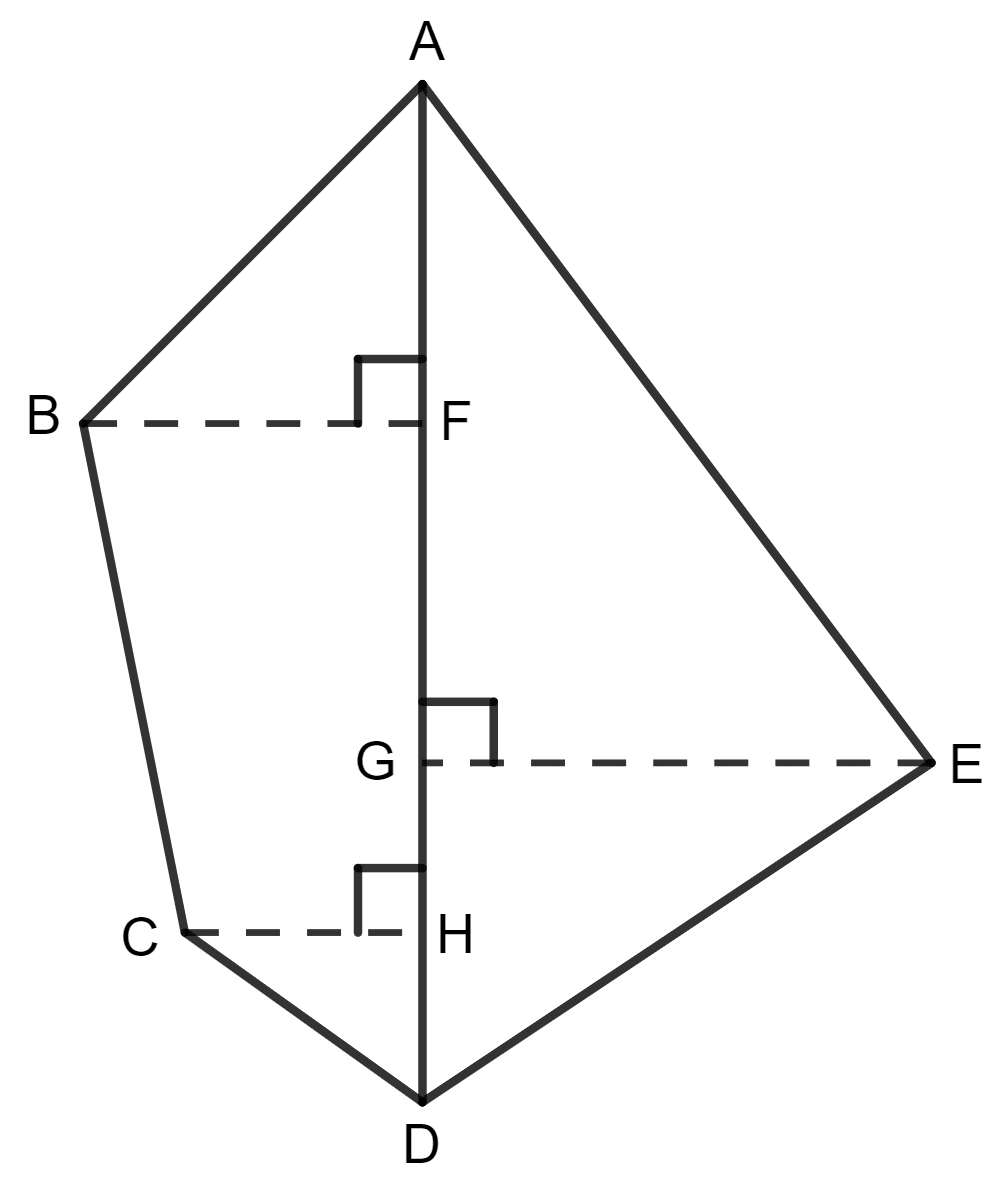
The given figure shows the cross-section of a concrete structure. Calculate the area of cross-section if AB = 1.8 m, CD = 0.6 m, DE = 0.8 m, EF = 0.3 m and AF = 1.2 m.
Mensuration
20 Likes
Answer
Given:
AB = 1.8 m, CD = 0.6 m, DE = 0.8 m, EF = 0.3 m and AF = 1.2 m
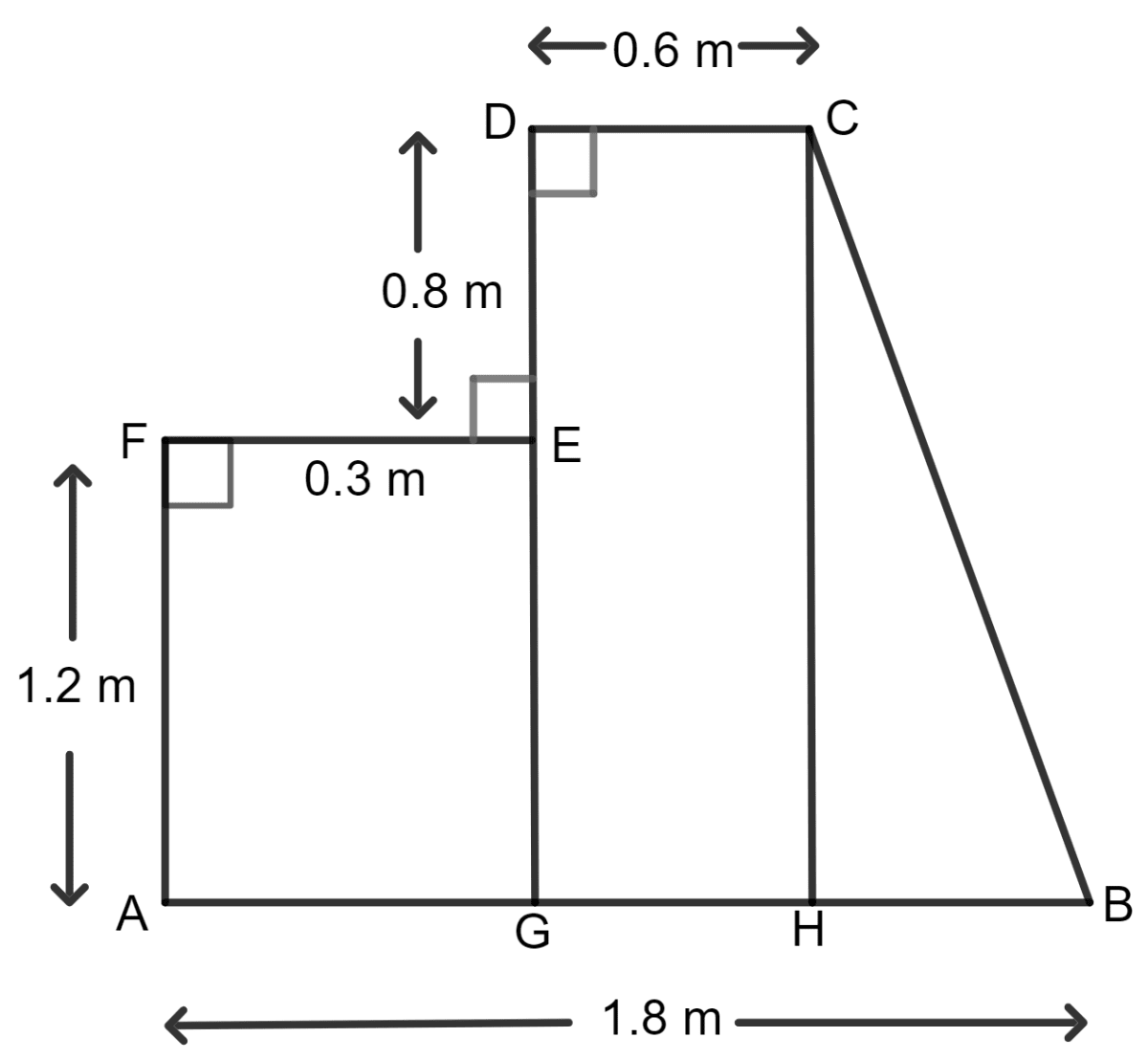
Area of ABCDEF = Area of rectangle AGEF + Area of rectangle GHCD + Area of triangle HBC.
Area of rectangle AGEF = l x b = AF x EF
= 1.2 x 0.3 m2
= 0.36 m2
Area of rectangle GHCD = l x b = GH x HC
= 0.6 x 2 m2 (HC = AF + ED = 1.2 + 0.8 = 2 cm)
= 1.2 m2
Area of triangle HBC = x b x h = x HB x HC
= x 0.9 x 2 m2 (HB = AB - AH = 1.8 - 0.9 = 0.9)
= 0.9 x 1 m2
= 0.9 m2
Now, area of ABCDEF = 0.36 m2 + 1.2 m2 + 0.9 m2
= 2.46 m2
Hence, the area of cross-section is 2.46 sq. m.
Answered By
9 Likes
Related Questions
The perimeter of a rhombus is 52 cm. If one diagonal is 24 cm; find :
(i) the length of its other diagonal,
(ii) its area.
The perimeter of a rhombus is 46 cm. If the height of the rhombus is 8 cm; find its area.
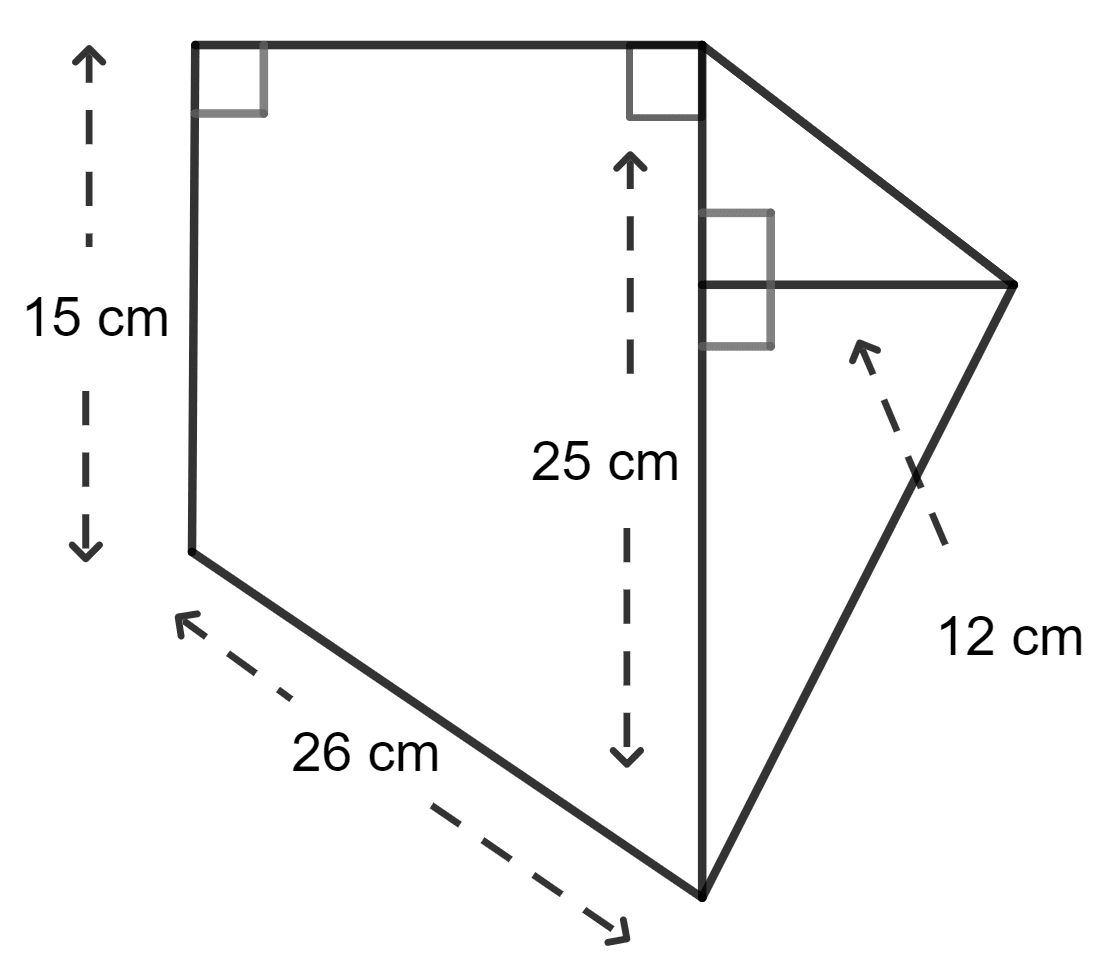
Calculate the area of the figure given below which is not drawn to scale.
The following diagram shows a pentagonal field ABCDE in which the lengths of AF, FG, GH and HD are 50 m, 40 m, 15 m and 25 m respectively; and the lengths of perpendiculars BF, CH and EG are 50 m, 25 m and 60 m respectively. Determine the area of the field.