Mathematics
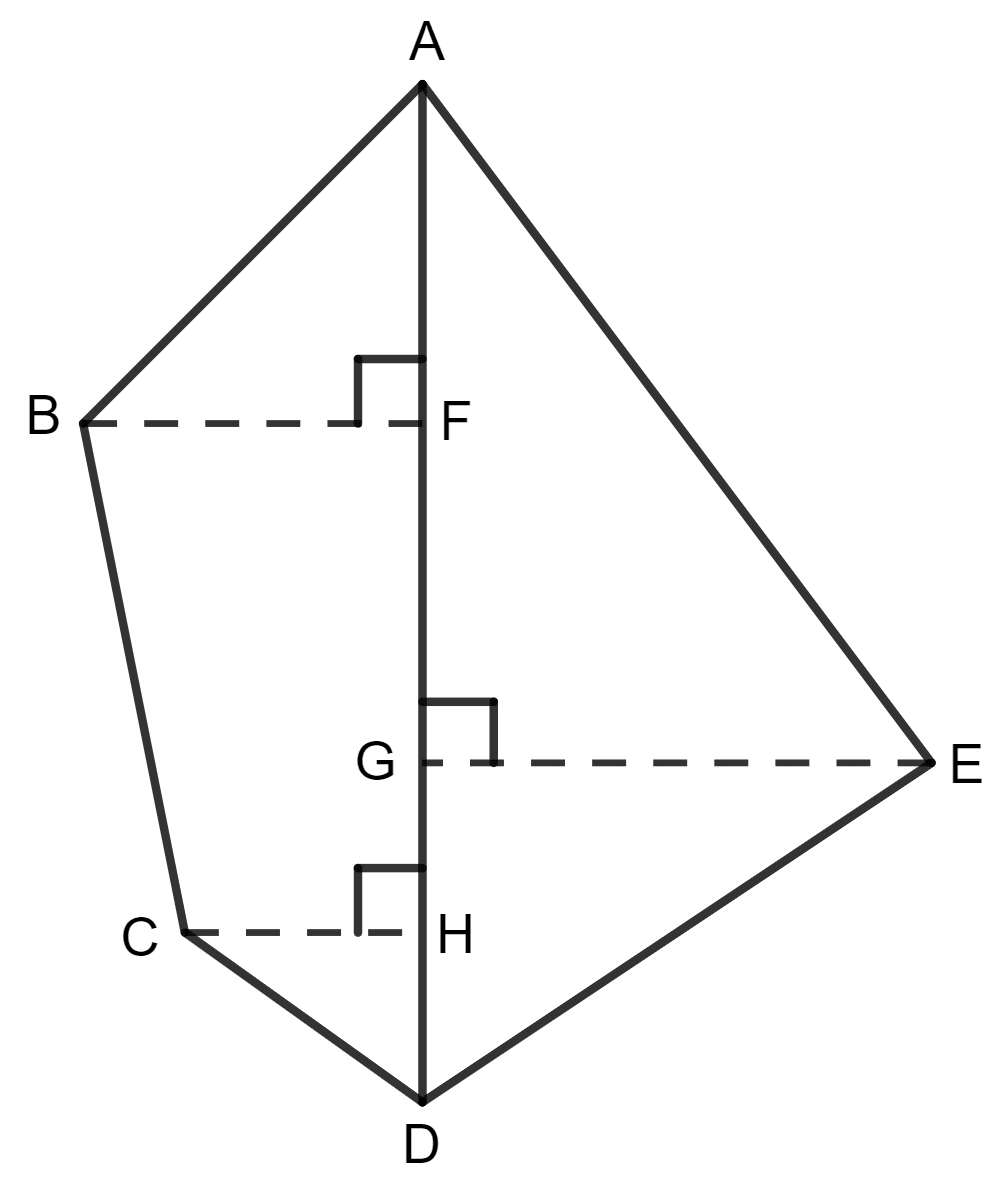
The following diagram shows a pentagonal field ABCDE in which the lengths of AF, FG, GH and HD are 50 m, 40 m, 15 m and 25 m respectively; and the lengths of perpendiculars BF, CH and EG are 50 m, 25 m and 60 m respectively. Determine the area of the field.
Mensuration
19 Likes
Answer
Area of figure ABCDE = Area of Δ ABF + Area of Δ AED + Area of Δ DHC + Area of trapezium BFHC
Area of Δ ABF = x b x h = x AF x BF
= x 50 x 50 m2
= 25 x 50 m2
= 1250 m2
Area of Δ AED = x b x h = x AD x GE
= x (AF + FG + GH + HD) x GE
= x (50 + 40 + 15 + 25) x 60 m2
= 130 x 30 m2
= 3900 m2
Area of Δ DHC = x b x h = x HD x CH
= x 25 x 25 m2
= 12.5 x 25 m2
= 312.5 m2
Area of trapezium BFHC = (sum of parallel sides) x distance between the parallel sides
= (BF + CH) x FH
= (BF + CH) x (FH + GH)
= (50 + 25) x (40 + 15) m2
= x 75 x 55 m2
= 37.5 x 55 m2
= 2062.5 m2
Thus, area of figure ABCDE = 1250 + 3900 + 312.5 + 2062.5 m2
= 7525 m2
Hence, the area is 7525 sq. m.
Answered By
14 Likes
Related Questions
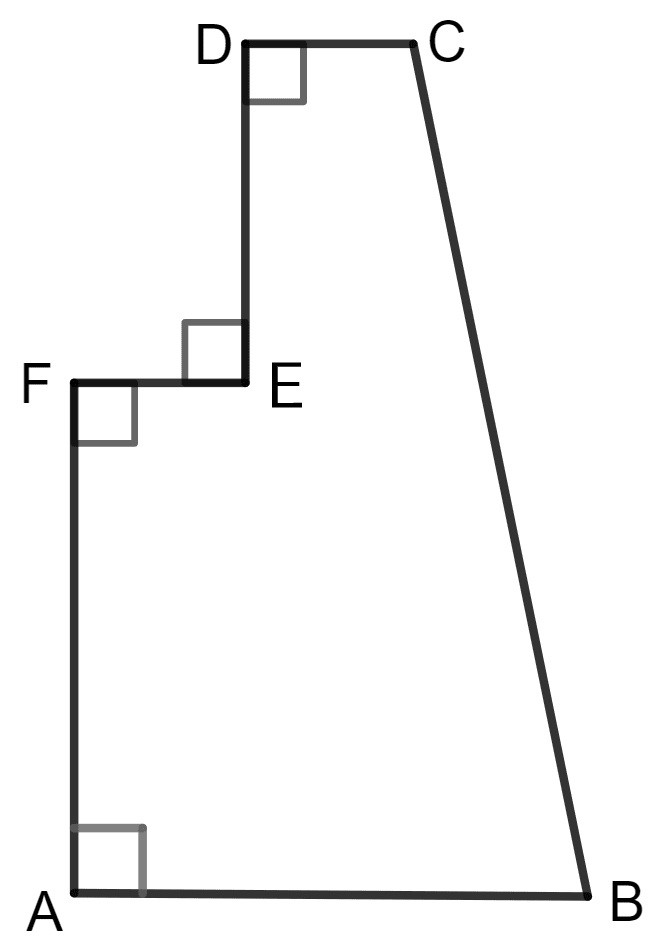
The given figure shows the cross-section of a concrete structure. Calculate the area of cross-section if AB = 1.8 m, CD = 0.6 m, DE = 0.8 m, EF = 0.3 m and AF = 1.2 m.
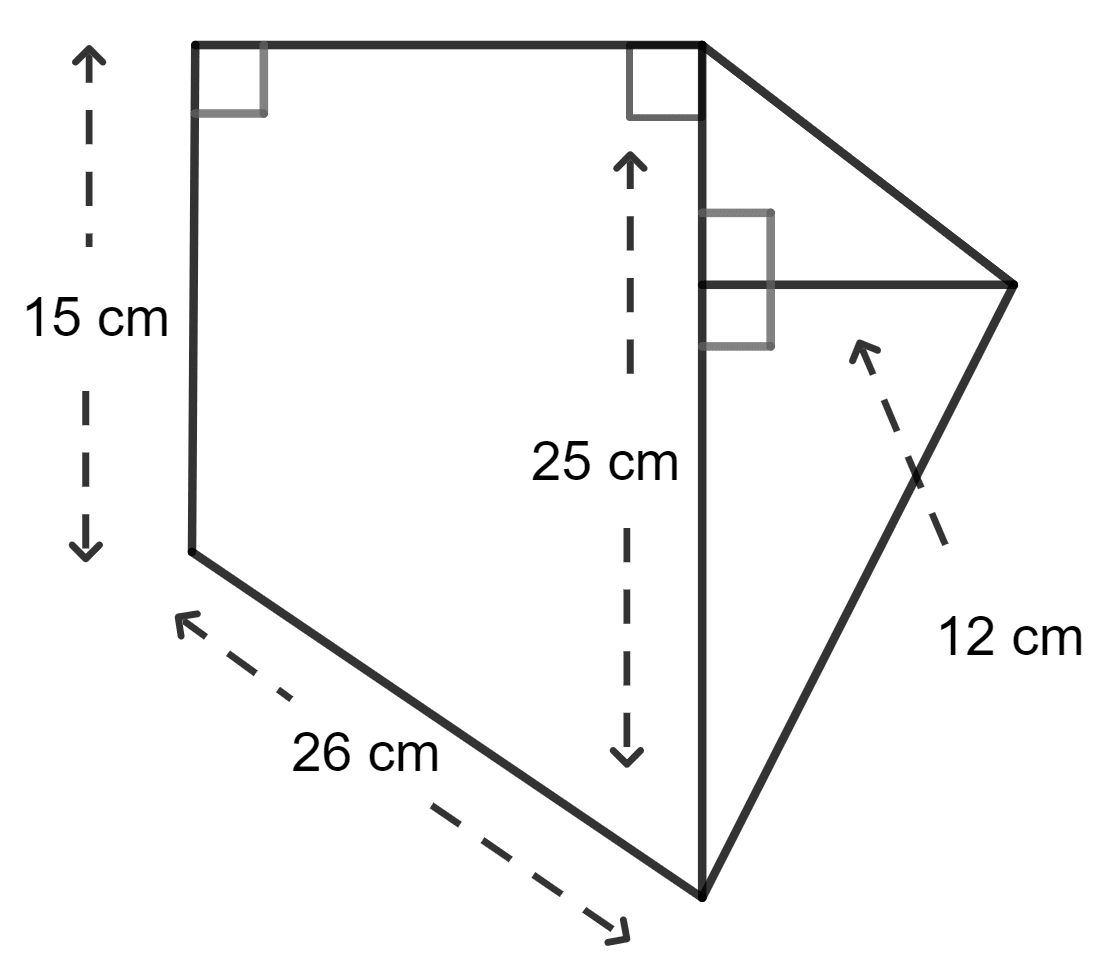
Calculate the area of the figure given below which is not drawn to scale.
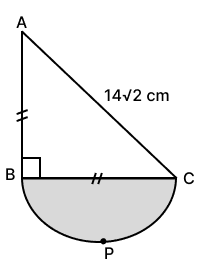
In the given figure, AB = BC, ∠ABC = 90°, AC = 14 cm and BPC (shaded portion) is semi-circle. If , the area of shaded portion is :
77 cm2
308 cm2
231 cm2
154 cm2
The diameter of a circle is 14 cm. If it is doubled, the perimeter of the resulting circle will become:
four times
doubled
halved
three times