Mathematics
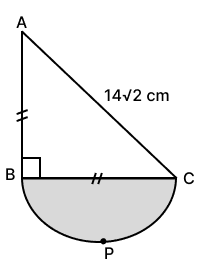
In the given figure, AB = BC, ∠ABC = 90°, AC = 14 cm and BPC (shaded portion) is semi-circle. If , the area of shaded portion is :
77 cm2
308 cm2
231 cm2
154 cm2
Mensuration
33 Likes
Answer
Let AB = BC = a cm and triangle ABC is a right triangle,
Using the Pythagoras theorem,
Base2 + Height2 = Hypotenuse2
⇒ BC2 + AB2 = AC2
⇒ a2 + a2 = ()2
⇒ 2a2 = 392
⇒ a2 =
⇒ a2 = 196
⇒ a =
⇒ a = 14 cm
Thus, AB = BC = 14 cm.
The diameter of the semicircle is BC = 14 cm, so the radius r is:
r = = = 7 cm
Area of semi-circle = πr2
Thus, the area of the shaded portion (the semicircle) is 77 cm2.
Hence, option 1 is the correct option.
Answered By
14 Likes
Related Questions
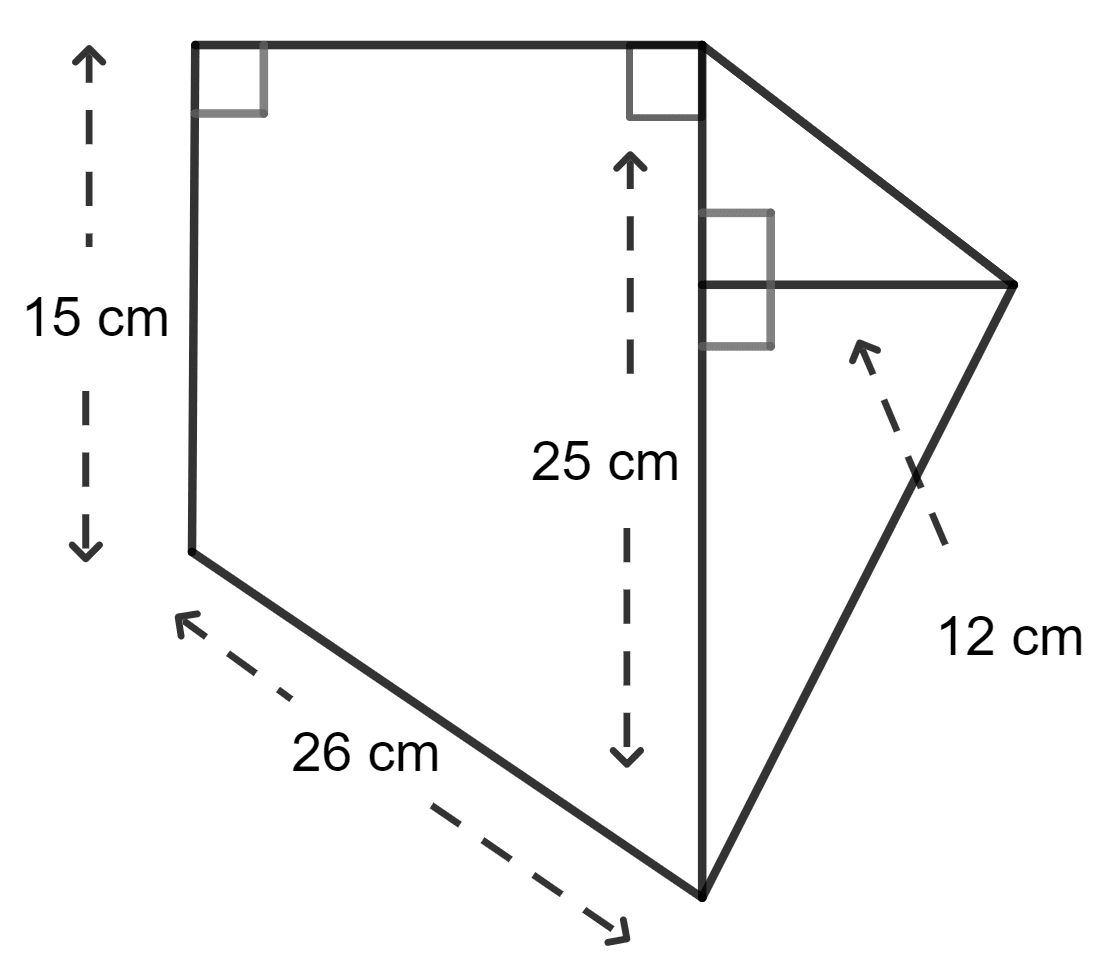
Calculate the area of the figure given below which is not drawn to scale.
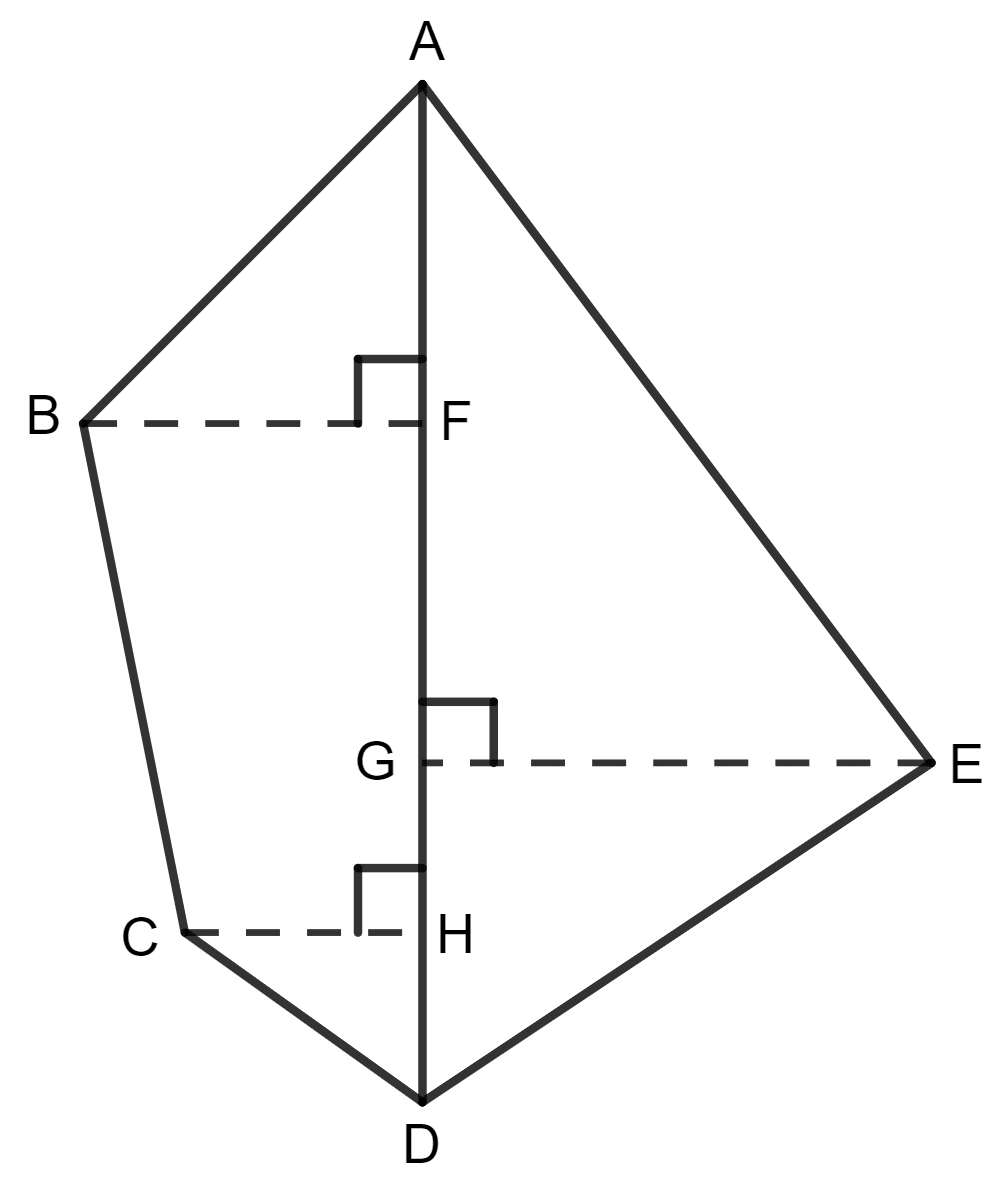
The following diagram shows a pentagonal field ABCDE in which the lengths of AF, FG, GH and HD are 50 m, 40 m, 15 m and 25 m respectively; and the lengths of perpendiculars BF, CH and EG are 50 m, 25 m and 60 m respectively. Determine the area of the field.
The diameter of a circle is 14 cm. If it is doubled, the perimeter of the resulting circle will become:
four times
doubled
halved
three times
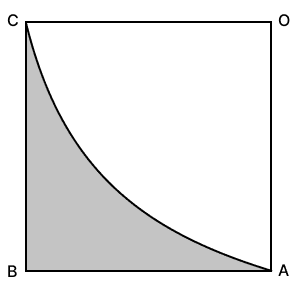
In the given figure, OABC is a square of side 14 cm. Taking , the area of the shaded portion is :
154 cm2
196 cm2
42 cm2
52 cm2