Mathematics
From the top of a tower 100 m high, a man observes the angle of depression of two ships A and B, on opposite sides of the tower as 45° and 38° respectively. If the foot of tower and the ships are in the same horizontal line, find the distance between two ships A and B to the nearest metre.
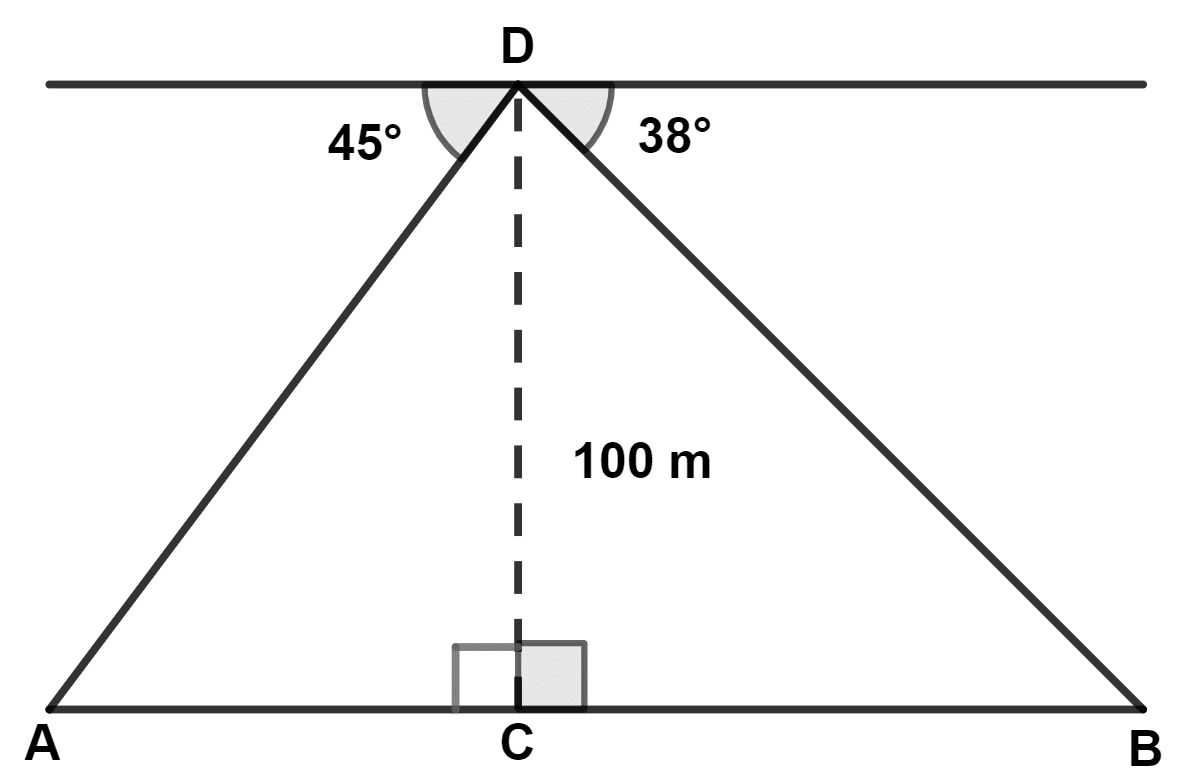
Heights & Distances
ICSE 2023
6 Likes
Answer
Let CD be the tower.
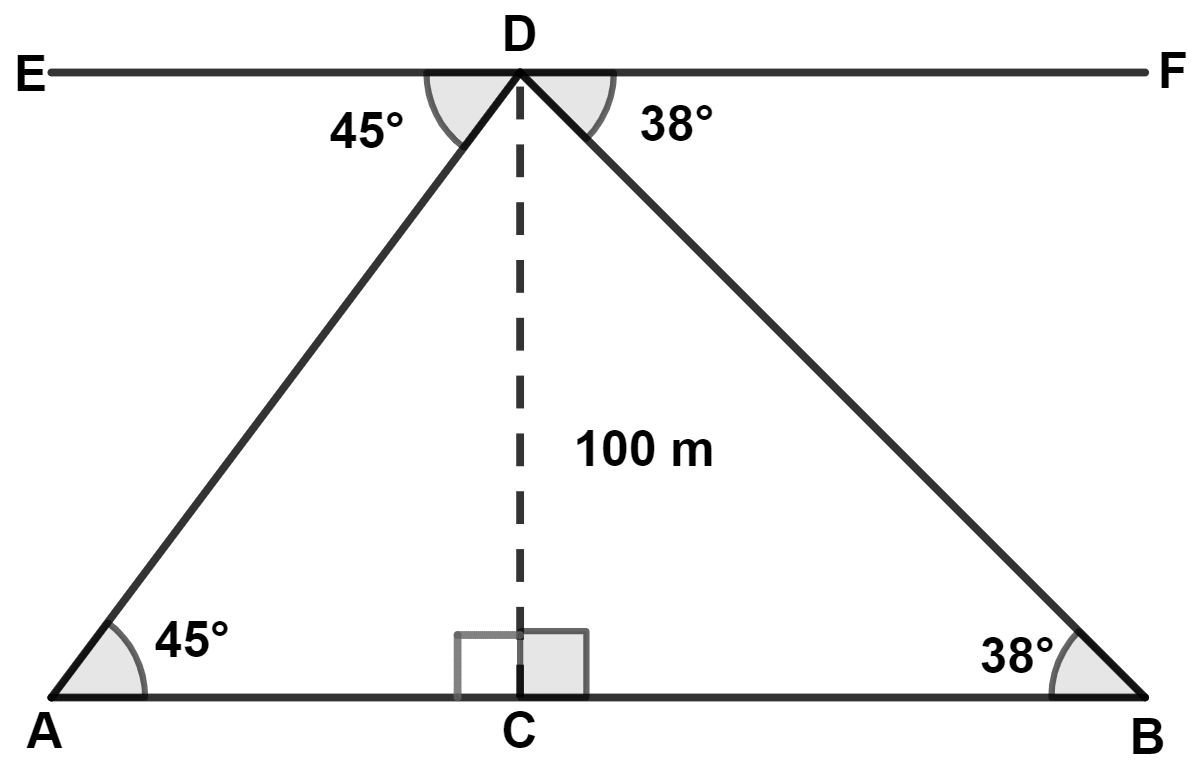
From figure,
⇒ ∠A = ∠EDA = 45° (Alternate angles are equal)
⇒ ∠B = ∠FDB = 38° (Alternate angles are equal)
In △ ACD,
⇒ tan A =
⇒ tan 45° =
⇒ AC = = 100 m.
In △ BCD,
⇒ tan B =
⇒ tan 38° =
⇒ BC = = 127.99 m.
From figure,
The distance between ships A and B = AC + BC
= 100 + 127.99
= 227.99 m ≈ 228 m.
Hence, the distance between the two ships A and B = 228 m.
Answered By
3 Likes
Related Questions
Using componendo and dividendo solve for x : .
Which term of the Arithmetic Progression (A.P.) 15, 30, 45, 60 ….. is 300 ? Hence find the sum of all terms of the Arithmetic Progression (A.P.).
Factorize completely using factor theorem : 2x3 - x2 - 13x - 6.
Use graph paper to answer this question.
During a medical checkup of 60 students in a school, weights were recorded as follows :
Weight (in kg) Number of students 28-30 2 30-32 4 32-34 10 34-36 13 36-38 15 38-40 9 40-42 5 42-44 2 Taking 2 cm = 2 kg along one axis and 2 cm = 10 students along the other axis draw an ogive. Use your graph to find the :
(a) median
(b) upper quartile
(c) number of students whose weight is above 37 kg.